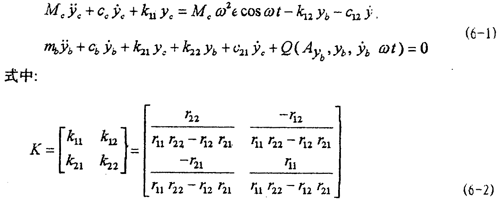第六章 帶有非線性聯軸器軸系的穩態響應計算實例
6-1 引言
本章將通過一個實例，用SSGILM法計算帶有非線性聯軸器軸系的強迫振動穩態響應，目的有三：一是驗證SSGILM法的有效性；二是考察聯軸器對軸系振動特性的影響；三是為下一章試驗研究做準備。
6-2 轉子軸系力學模型與運動微分方程的建立
本章研究的對象為一個置于外伸軸中的單圓盤轉子軸系，如圖6-1所示。
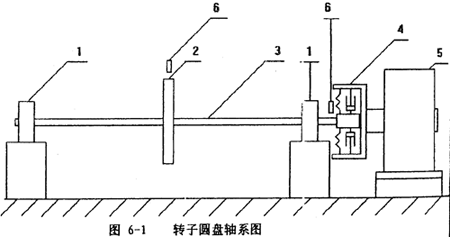
圓盤2安裝在轉軸兩支承1的中間位置，軸3一端由具有非線性特性的聯軸器4與電動機5聯結。轉軸的兩個支承1中的軸承為雙列向心球面球軸承，軸可以在軸承內自由偏轉。圓盤靠軸套與軸相聯，由于軸套有一定的長度和直徑，它對轉軸柔度及剛度均有影響，但影響有多大，有待實際計算中考察，故在此先視轉軸為一變截面（階梯）細長軸。同時考慮轉軸質量對軸系固有頻率的影響。根據第五章建立軸系力學模型的原則，可以將圖6-1所示軸系處理成為兩個自由度系統，然后根據第五章的式（5-4）、（5-5）可以寫出轉子軸系的振動微分方程式：
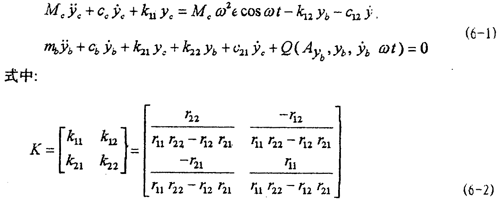
式中的r11，r12，r21，r22為轉軸的柔度系數，計算公式見附錄1。
yc為圓盤在y軸方向的位移，
c=dyc/dt，
c=d2yc/dt2，分別為圓盤在y軸方向的速度和加速度，yb，b=dyb/dt，b= d2yb/dt2，分別為聯軸器從動端質量塊mb在y軸方向的位移、速度和加速度。k11，k 12，k 21，k 22為轉軸的剛度系數，cc,cb,c12,c21為轉軸的阻尼系數，Q為聯軸器恢復力。Mc=mc+ms，ms為轉軸及軸套的質量，mc為圓盤的質量，ω為轉軸的角速度。
6-3 應用SSGILM法計算轉子軸系的穩態響應
按第五章提出的SSGILM法及求解步驟，編制了求解轉子軸系穩態響應的大型計算機軟件，并在386徽機上得到實現。
計算所用的各數據（見附錄圖1）為：
l=1325mm，l2=45mm，l1=（l-2l2）/2mm，l=30mm
Mc=36.4kg e=0.55mm a=150mm cc=cb=0.001
{a}的初始值任意取為（N=8）：
表6-1 {a}初值表
| a0 |
|
a1 |
 |
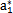a2 |
 |
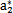a3 |
 |
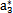a4 |
 |
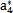| 0.0 |
|
0.5 |
0.3 |
0.4 |
0.2 |
0.1 |
0.1 |
0.08 |
0.07 |
| a5 |
 |
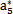a6 |
 |
a7 |
 |
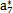a8 |
 |
|
|
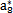| 0.06 |
0.05 |
0.04 |
0.03 |
0.02 |
0.01 |
0.009 |
0.0 |
|
|
實際計算表明軸套對軸系振動特性的影響不大，轉軸可視為等截面軸。
6-4 理論計算結果分析
將計算所得數據畫成曲線，如圖6-2（a）～（d）。圖中A表示幅值，Ayc表示位移yc的幅值，Ayb表示位移yb的幅值，Ayc1表示軸系振動微分方程形式（6-1）第一式中等號右邊恢復力產生的位移yc1的幅值，Ayc2表示式（6-1）第一式中等號右邊圓盤質量偏心力激勵作用下產生的位移yc2幅值。
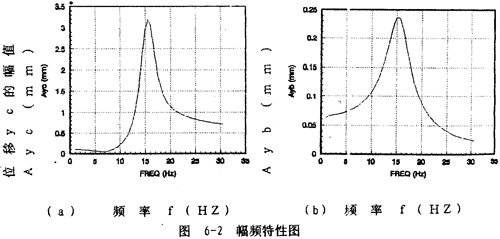
從圖6-2（a）可以知道軸系在圓盤質量偏心力激勵作用下，圓盤在y方向的振動位移幅值Ayc從1赫茲開始隨著頻率的增加而有微量減小直至7赫茲，在此之后，位移幅值隨頻率增大而迅速增大直至軸系的一個固有頻率15.56赫茲處，然后位移幅值隨頻率增大而減小并趨于某一定值。由第五章中的式（5-4）、（5-6）、（5-11）、（5-12）以及本章中的式（6-1）第一式可知，圓盤的振動位移yc是由兩部分激勵力激勵產生的，一部分是Mcω2ecosωt激勵力，它產生振動位移yc2，另一部分是（-k12yb-c12b）恢復力激勵，它產生振動位移yc1,因此圓盤的振動位移yc=yc1+yc2。
從圖6-2(b）可以知道，聯軸器從動端質量塊mb的位移幅值Ayb從1赫茲開始隨頻率增大而迅速增大直至軸系的一階固有頻率15.2赫茲，然后隨頻率增大而迅速減小，在一階固有頻率處達到最大值。
位移幅值Ayc1隨頻率變化的規律可以從圖6-2（c）看到。Ayc1從1赫茲開始隨頻率增大而增大，在軸系的一階固有頻率處達到最大值，然后隨頻率增大而減小直至趨于零。Ayc1隨頻率的變化規律反映聯軸器對圓盤振動位移幅值Ayc1的影響部分。
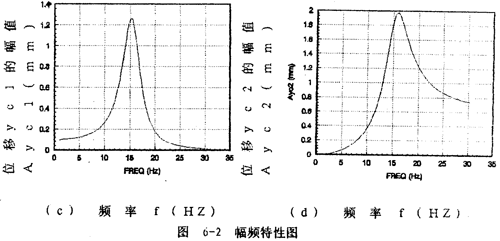
yc2的幅頻特性如圖6-2(d）所示。Ayc2從1赫茲開始隨頻率的增大而迅速增大，在軸系的二階固有頻率15.56赫茲處達到最大值，然后隨頻率增大而減小并趨于某一定值，Ayc2隨頻率變化的規律反映圓盤僅在質量偏心激勵下，而軸系沒有鋼絲繩聯軸器影響時圓盤的幅頻特性。考慮上聯軸器對圓盤幅頻特性的影響部分Ayc1（圖6-2(c）所示部分），則圓盤的幅頻特性即為圖6-2(a）所示。由此可見，鋼絲繩聯軸器在頻率的較低段（0～11赫茲）對圓盤振動有抑制作用。值得一提的是Ayc不是Ayc1和Ayc2的簡單相加，而與各頻率對應的向量{a}中17個元素以及相位有關。
為了比較各幅頻曲線的相對大小以及討論鋼絲繩聯軸器對軸系振動特性的影響，畫出各幅頻曲線相對大小的比較圖如圖6-3（a）～（b）所示。
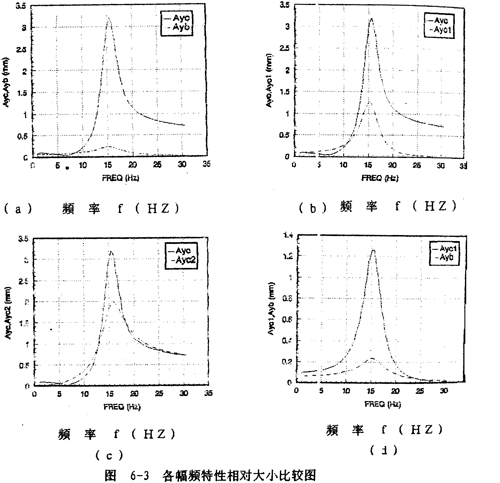
從圖6-3（a）可知，聯軸器從動端質量塊mb的振幅Ayb（虛線）相對圓盤振幅Ayc（實線）來說是很小的。它們各自在一、二階固有頻率處達最大值。
圖6-3（b）表示圓盤振幅Ayc（實線）與聯軸器引起的圓盤振幅分量Ayc1（虛線）的相對大小比較圖。圖6-3（c）表示圓盤振幅Ayc（實線）與圓盤質量偏心引起的圓盤振幅分量Ayc2（虛線）的相對大小比較圖。圖6-3（d）展示了聯軸器引起的圓盤振幅分量Ayc1（實線）與聯軸器振幅Ayb（虛線）的比較圖。從圖6-3（b）、（c）可知，圓盤偏心質量引起的圓盤振動位移分量yc2的幅值Ayc2（虛線）大于聯軸器引起的圓盤振動位移分量yc1的幅值Ayc1（虛線）。從這兩圖中曲線的比較還可以知道，鋼絲繩聯軸器對圓盤振幅的影響在不同頻率段效果是不相同的。總的來說，在頻率12.7～18.3赫茲區域外，聯軸器對圓盤振動是起減振作用的，這一特性可以從圖6-13（c）清楚地看到。但在此頻率范圍內，聯軸器對圓盤振動是增大作用的。
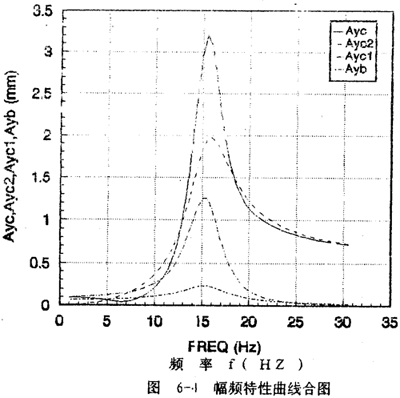
從圖6-4各幅頻曲線的合圖，可以清楚地看到，聯軸器從動端質量塊mb的振動位移幅值Ayb和聯軸器在圓盤上引起的圓盤振動位移分量Ayc1的最大值均出現在軸系一階固有頻率處，而圓盤振動位移幅值Ayc和圓盤質量偏心引起的圓盤振動位移幅值分量Ayc2的最大值均出現在軸系二階固有頻率處，兩個固有頻率相距較近。
6-5 小結
經過以上實例計算和結果分析可以得出以下結論：
1.用SSGILM法編制的程序從任選的初始值{a（0）}開始進行逼近搜索迭代計算，計算結果表明SSGILM法明顯地改變了LM法對初始值要求高的缺點，從任意給定的初始值{a（0）}開始自動逼近搜索，可以很快地收斂于滿足精度的{a}值。
2.鋼絲繩聯軸器對圓盤振動的影響，在不同的頻率段有不同的效果，在軸系固有頻率附近區域內，鋼絲繩聯軸器使圓盤振動位移幅值增大，而在軸系固有頻率附近區域外。聯軸器對圓盤振動具有抑制作用。
3.在整個計算頻帶，聯軸器振動位移幅值相對于圓盤振動位移幅值來說很小。
4.SSGILM法能夠計算出軸系的一階固有頻率（對應于聯軸器），彌補了多自由度非線性系統不能顯式計算（對應于聯軸器的）固有頻率的不足。
上一頁
下一頁
