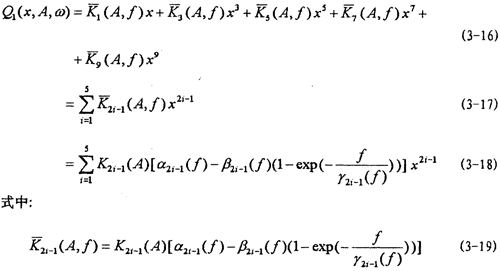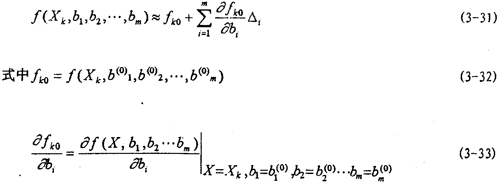二、考慮頻率影響的數(shù)學(xué)模型
在這種情況下,聯(lián)軸器的數(shù)學(xué)模型的表達(dá)式為(3-7)式,下面分別討論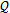 l和
l和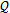 2函數(shù)表達(dá)式的結(jié)構(gòu)形式:
2函數(shù)表達(dá)式的結(jié)構(gòu)形式:
1.非遲滯非線性彈性恢復(fù)力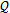 l的數(shù)學(xué)模型
l的數(shù)學(xué)模型
由試驗(yàn)研究知道,聯(lián)軸器的彈性恢復(fù)力不僅是振幅的的函數(shù)而且還是頻率的函數(shù),隨著頻率的增大,在一定頻率范圍內(nèi),彈性恢復(fù)力逐漸減小,然后趨于一定值,根據(jù)這一特性,在建造彈性恢復(fù)力新的數(shù)學(xué)模型時(shí),引進(jìn)一個(gè)能描述這一特性的指數(shù)函數(shù)項(xiàng)e-flr(f),這樣,新構(gòu)建的彈性恢復(fù)力數(shù)學(xué)模型為:
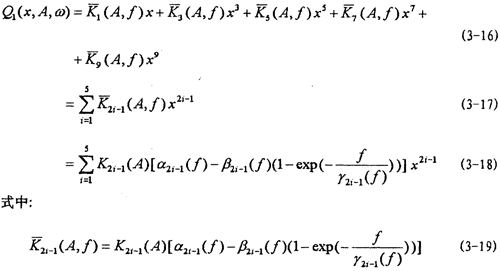
同時(shí),定義幾個(gè)新函數(shù)參數(shù),a2i-1(f)為剛度幅值頻率影響系數(shù),它表示聯(lián)軸器彈性元件各階剛度的幅值受頻率變化影響的程度;β2i-1(f)稱為剛度幅值頻率衰減系數(shù),表示彈性元件各階剛度的幅值隨頻率增加的衰減程度;y2i-1(f)稱為剛度頻率衰減系數(shù),表示彈性元件各階剛度隨頻率增加的衰減速率,y2i-1(f)愈大,剛度值隨頻率減小的速度就愈慢,反之,則愈快。從理論上講,只有當(dāng)f值趨于無窮大時(shí),exp{-f/[ y2i-1(f)]}才趨于零,各階剛度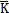 2i-1(A,f)才趨于各自的定值K2i-1(A)[α2i-1(f)-β2i-1(f)]。但事實(shí)上,由于指數(shù)曲線開始變化較大,而后逐漸緩慢,所以,實(shí)際上f達(dá)到一定值后,exp{-f/[ γ2i-1(f)]}已經(jīng)很小了,例如,設(shè)f=5 γ2i-1(f),這時(shí)有:
2i-1(A,f)才趨于各自的定值K2i-1(A)[α2i-1(f)-β2i-1(f)]。但事實(shí)上,由于指數(shù)曲線開始變化較大,而后逐漸緩慢,所以,實(shí)際上f達(dá)到一定值后,exp{-f/[ γ2i-1(f)]}已經(jīng)很小了,例如,設(shè)f=5 γ2i-1(f),這時(shí)有:
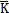 2i-1(A,f)= K2i-1(A)[α2i-1(f)-β2i-1(f)(1-e-5)]
2i-1(A,f)= K2i-1(A)[α2i-1(f)-β2i-1(f)(1-e-5)]
= K
2i-1(A)[α
2i-1(f)-β
2i-1(f)×0.99326] (3-20)
當(dāng)頻率f=8,10,…,30赫茲時(shí),剛度不再隨頻率的變化而變化,由此可得γ2i-1(f)=1,6,2,…,6;α2i-1(f)-β2i-1(f)×0.99326=βc,這些參數(shù)值和關(guān)系式在辨識(3-19)式中參數(shù)時(shí),可作為已知條件應(yīng)用。
從以上分析可知,(3-18)式表示的數(shù)學(xué)模型能客觀地反映聯(lián)軸器彈性恢復(fù)力隨振幅和頻率變化的規(guī)律。
2.遲滯非線性阻尼力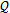 2的數(shù)學(xué)模型
2的數(shù)學(xué)模型
當(dāng)同時(shí)考慮振幅和頻率對遲滯阻尼力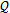 2的影響時(shí),
2的影響時(shí),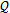 2將是振幅和頻率的函數(shù),如果經(jīng)過參數(shù)辨識說明(3-14)形式的數(shù)學(xué)模型能合理地描述阻尼力,那么,在同時(shí)計(jì)及振幅和頻率對遲滯阻尼力
2將是振幅和頻率的函數(shù),如果經(jīng)過參數(shù)辨識說明(3-14)形式的數(shù)學(xué)模型能合理地描述阻尼力,那么,在同時(shí)計(jì)及振幅和頻率對遲滯阻尼力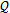 2的影響時(shí),我們?nèi)越⑦t滯阻尼力的數(shù)學(xué)模型表達(dá)式為(3-14)式的形式,不過其中各系數(shù)不僅是振幅A的函數(shù)而且還是頻率f的函數(shù),建立的第二種數(shù)學(xué)模型仍以等效粘性阻尼來描述遲滯非線性阻尼,與(3-15)式所不同的是,在此建立聯(lián)軸器阻尼耗能的函數(shù)時(shí),同時(shí)考慮聯(lián)軸器遲滯回線面積隨振幅A和頻率f變化的規(guī)律,而在建立(3-15)式時(shí)僅考慮聯(lián)軸器遲滯回線面積隨振幅A的變化規(guī)律。為了敘述方便,這些問題在參數(shù)辨識一節(jié)中討論。這樣,這二種阻尼力模型為:
2的影響時(shí),我們?nèi)越⑦t滯阻尼力的數(shù)學(xué)模型表達(dá)式為(3-14)式的形式,不過其中各系數(shù)不僅是振幅A的函數(shù)而且還是頻率f的函數(shù),建立的第二種數(shù)學(xué)模型仍以等效粘性阻尼來描述遲滯非線性阻尼,與(3-15)式所不同的是,在此建立聯(lián)軸器阻尼耗能的函數(shù)時(shí),同時(shí)考慮聯(lián)軸器遲滯回線面積隨振幅A和頻率f變化的規(guī)律,而在建立(3-15)式時(shí)僅考慮聯(lián)軸器遲滯回線面積隨振幅A的變化規(guī)律。為了敘述方便,這些問題在參數(shù)辨識一節(jié)中討論。這樣,這二種阻尼力模型為:

綜上所述,將(3-12)式與(3-18)式比較,將(3-14)~(3-15)式與(3-21)~(3-22)對應(yīng)式比較可知,后者同時(shí)考慮了振幅A和頻率f對聯(lián)軸器恢復(fù)力的影響,因而適用范圍較前者僅考慮振幅A的影響時(shí)更大,但后都數(shù)學(xué)表達(dá)式復(fù)雜,大大地增加了參數(shù)的辨識難度。由試驗(yàn)研究知,頻率變化對恢復(fù)力影響范圍較小,為了簡化計(jì)算用(3-12)和(3-14)~(3-15)較好。
3-4 聯(lián)軸器數(shù)學(xué)模型參數(shù)辨識
本節(jié)將利用試驗(yàn)數(shù)據(jù),根據(jù)上節(jié)建立的聯(lián)軸器恢復(fù)力數(shù)學(xué)模型的類型,聯(lián)分別選用線性參數(shù)辨識方法和非線性參數(shù)辨識方法,按最小二乘法原理,辨識聯(lián)軸器數(shù)學(xué)模型中的參數(shù),找出各參數(shù)與振幅和頻率的關(guān)系,得到聯(lián)軸器恢復(fù)力由彈性和阻尼力描述的函數(shù)關(guān)系式。
一、參數(shù)辨識的難點(diǎn)
聯(lián)軸器數(shù)學(xué)模型函數(shù)關(guān)系的復(fù)雜性以及函數(shù)關(guān)系式中參數(shù)的非線性都給參數(shù)辨識工作帶來困難。針對這些情況,對數(shù)學(xué)模型中某些參數(shù)隨振幅和頻率變化規(guī)律還不能給出表達(dá)式時(shí),我們先求出這些模型在不同振幅和頻率下,各參數(shù)隨振幅和頻率變化的離散值,然后根據(jù)這些離散值隨振幅和頻率變化的規(guī)律,來定出函數(shù)表達(dá)式,在此基礎(chǔ)上再進(jìn)一步找出這些參數(shù)與振幅和頻率的函數(shù)關(guān)系,最后得到聯(lián)軸器恢復(fù)力與振幅、頻率、位移和速度的表達(dá)式。
二、參數(shù)辨識
1.辨識不考慮頻率影響數(shù)學(xué)模型的參數(shù)
不考慮頻率影響時(shí)聯(lián)軸器的數(shù)學(xué)模型為(3-12)~(3-15)式,
a.非線性彈性恢復(fù)力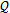 l數(shù)學(xué)模型中參數(shù)的辨識
l數(shù)學(xué)模型中參數(shù)的辨識
此中情況下, l的表達(dá)式為(3-12)和(3-13)式。由這兩式可知,模型中含有九階的高次非線性彈性力,其各階動(dòng)剛度K2i-1 (A)是振幅的函數(shù),數(shù)學(xué)模型為一個(gè)n′階的冪函數(shù)多項(xiàng)式,K2i-1 (A)是各參數(shù)b0,2i-1~bn,2i-1 (i=1,2,…,5)的線性函數(shù)。于是各階動(dòng)剛度K2i-1 (A)中各參數(shù)辨識可歸結(jié)以下最小二乘法問題:
l的表達(dá)式為(3-12)和(3-13)式。由這兩式可知,模型中含有九階的高次非線性彈性力,其各階動(dòng)剛度K2i-1 (A)是振幅的函數(shù),數(shù)學(xué)模型為一個(gè)n′階的冪函數(shù)多項(xiàng)式,K2i-1 (A)是各參數(shù)b0,2i-1~bn,2i-1 (i=1,2,…,5)的線性函數(shù)。于是各階動(dòng)剛度K2i-1 (A)中各參數(shù)辨識可歸結(jié)以下最小二乘法問題:
已知K2i-1 (A)是關(guān)于自變量X=[A,A2,…An′]T和待定參數(shù)B=[ b0,2i-1,b1,2i-1,…,bn′,2i-1]T的形式已知的函數(shù)(3-13),簡寫成:
K2i-1 (A)=f(X,B) (3-23)
今給出(X,K2i-1 )的n對試驗(yàn)值:
(XK,K2i-1,K) (k=1,2,…,n) (3-24)
要求確定參數(shù)B使

得一組線性方程組,在n>k的情況下,聯(lián)立求解這一線性方程組即可求得唯一的一組B值。根據(jù)此法求得(3-13)式中參數(shù)值并代回可得:


將(3-27)式中剛度函數(shù)作成曲線如圖3-3(a)-(e)所示,由一階動(dòng)剛度函數(shù)圖3-3(a)可知,振幅在lmm~2mm范圍內(nèi)時(shí),動(dòng)剛度隨振幅增大而增大,呈硬特性;當(dāng)振幅在2mm~7mm范圍內(nèi)時(shí),動(dòng)剛度隨振幅增大而減小,呈軟特性;當(dāng)振幅在7mm~8mm范圍時(shí),動(dòng)剛度隨振幅增大略有回升。由此圖可知,在聯(lián)軸器初始小振幅和極限振幅附近范圍內(nèi),動(dòng)剛度呈硬特性,而在中間振幅范圍內(nèi)呈軟特性。K5(A)和K9(A)也具有類似的特性。而K3(A)和K7(A)在小振幅時(shí)呈軟特性,這樣的動(dòng)剛度特性滿足船舶緩沖減振降噪的要求,即在一般低能量風(fēng)浪流作用下,該聯(lián)軸器鋼絲繩元件的變形小,動(dòng)剛度大,呈硬特性,這能保證船舶推進(jìn)軸系的基頻高于風(fēng)浪流的顯著能量頻率;在大能量風(fēng)浪流和沖擊作用下時(shí),聯(lián)軸器由于載荷增大而變形增大,這種情況下動(dòng)剛度軟化,使船舶推進(jìn)軸系頻率變小,向遠(yuǎn)離大能量風(fēng)浪流和沖擊顯著能量頻率一側(cè)偏移,在遲滯阻尼下耗散能量,使軸系沖擊振動(dòng)響應(yīng)降低。由(3-27)式和(3-12)式可作出相應(yīng)的彈性恢復(fù)力單值曲線如圖3-4所示。將圖3-4中代表彈性恢復(fù)力的單值曲線與圖3-2中的單值曲線比較可知,(3-12)式能較好地描述聯(lián)軸器彈性恢復(fù)力隨振幅變化的規(guī)律。
b.非線性阻尼力數(shù)學(xué)模型中參數(shù)的辨識
此情況下,建立了二種數(shù)學(xué)模型(3-14)式和(3-15)式。對于(3-14)式描述的模型, 2是參數(shù)n的非線性函數(shù),因此,在進(jìn)行參數(shù)辨識時(shí),需要用非線性參數(shù)的辨識方法。此時(shí),這種模型中各參數(shù)的辨識可歸結(jié)為如下的最小二乘法問題:
2是參數(shù)n的非線性函數(shù),因此,在進(jìn)行參數(shù)辨識時(shí),需要用非線性參數(shù)的辨識方法。此時(shí),這種模型中各參數(shù)的辨識可歸結(jié)為如下的最小二乘法問題:
已知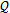 2是關(guān)于自變量X=[x1,x2,…,xp]T和待定參數(shù)B=[b1,b2,…,bm]T的形式已知函數(shù)(3-14)式,簡寫成:
2是關(guān)于自變量X=[x1,x2,…,xp]T和待定參數(shù)B=[b1,b2,…,bm]T的形式已知函數(shù)(3-14)式,簡寫成:
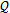 2=f(X,B) (3-28)
2=f(X,B) (3-28)
對于給定的n組試驗(yàn)數(shù)據(jù)值(Xk,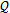 2k),要求確定參數(shù)B使
2k),要求確定參數(shù)B使

為最小。對于這種非線性參數(shù)識別,很難直接進(jìn)行求解,通常采用逐次逼近的方法處理,在此采用高斯-牛頓法來辨識。高斯-牛頓法的基本思想是:先給出各參數(shù)bi的一個(gè)初始值,記為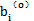 ,初值與真值之差為△i,即有:
,初值與真值之差為△i,即有:
bi=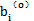 +△i (i=1,2,…,m) (3-30)
+△i (i=1,2,…,m) (3-30)
這樣,確定bi的問題就變成了確定△i的問題。為確定bi,在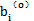 鄰域內(nèi)將函數(shù)f(X,B)作代臺勞級數(shù)展開,并略去△i的二次及二次以上項(xiàng)得:
鄰域內(nèi)將函數(shù)f(X,B)作代臺勞級數(shù)展開,并略去△i的二次及二次以上項(xiàng)得:
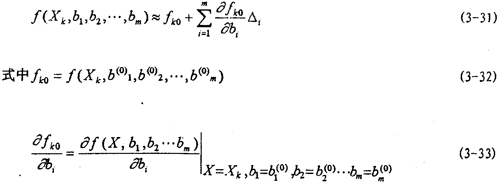
上一頁
下一頁