第3章 三叉桿式萬向聯軸器的理論運動分析
3.1 前言
三叉桿式萬向聯軸器是一種新型的萬向聯軸器，它在結構上簡單、緊湊、安裝方便，具有承載能力大和工作可靠等優點。在國外已廣泛地被應用于汽車工業和其它的工業領域。但由于它的運動規律復雜，為了徹底弄清它的特點，長期以來一直都有人對它運用不同的計算方法進行運動分析。本章運用方向余弦矩陣這一數學工具，對三叉桿滑移式萬向聯軸器運動機理進行解析計算，得出它的運動規律表達式和曲線圖，并在后面的章節中運用同樣的結構進行仿真驗證，以檢驗計算的正確性。
3.2 三叉桿式萬向聯軸器的理論運動分析
3.2.1 三叉桿滑移式萬向聯軸器簡介
三叉桿滑移式萬向聯軸器由滑桿套軸（又稱為輸入軸）、三叉桿（又稱為輸出軸）、小桿和內球頭等組成產（這幾個構件的模型圖3-1所示），其中小桿和內球頭裝配成滑桿（模型的裝配關系如圖3-l最上部），在這種連接形式下，內球頭可在小桿內轉動，即形成球面副，具有三個轉動自由度。在滑桿套軸上有三個均勻分布的孔（小桿的滑道），與安裝在三叉桿軸頸上的滑桿相配合，這里所有的配合均為間隙配合。當三叉桿萬向聯軸器運轉時（兩軸有夾角），滑桿一方面沿滑道的中心線移動，另一方面沿三叉桿軸頸移動，從而實現運動過程中的角度補償。
3.2.2 分析模型的建立
由于運動規律的特殊性，為了實現它的運動，對單聯的三叉桿式萬向聯軸器需要在輸出軸上安裝調心軸承（調心軸承的模型裝配關系如圖3-1所示，它的內圈同三叉桿無相對滑動），否則它在理論上是不可以轉動的（自由度不夠）。再裝上機架，即左支承（如圖3-1)，就構成了三叉桿滑移式萬向聯軸器的裝配模型。其模型如圖3-2所示。
通過對圖3-2中的模型進行抽象，可得到三叉桿滑移式萬向聯軸器的機構運動簡圖，其示意圖如圖3-3所示，在此模型中關節軸承中心同三叉桿三軸頸軸線的交點距離一直不變。由以前的分析可知，在這種模型中，三叉桿中心的運動軌跡在輸出軸平行于自身運動時是以
P=
（
）為半徑的圓，其中R為輸入軸滑道軸線到輸入軸軸線的距離（圖3-4中有其示意），β為輸入、輸出兩軸線之間的夾角（圖3-5中有其示意）,L為圓錐擺中軸線長。所以采用調心軸承安裝輸出軸時，輸出軸的運動必為一圓錐擺運動，三叉桿中心的偏心距ρ與比值
有關。當L為無窮大時，ρ=（），這時相當于用雙向心軸承安裝輸出軸，隨著增大，ρ的計算值與實際值將會出現微小的誤差；由于誤差極小，所以在一般應用場合可以取ρ≈（）。
由于在轉動的過程中，三叉桿交點作旋轉運動，因此會導致輸入軸與輸出軸之間的夾角發生變化，其變化范圍為βmin～βmax，當O點（見圖3-5）處于輸入軸與輸出軸轉動錐中心線所構成平面的兩個極限位置時，偏轉角達到兩極值:
在其它位置時，偏轉角介于兩者之間。
3.2.3 坐標系的建立
由于輸出軸作一圓錐運動，在分析的過程中需建立三套坐標系，如圖3-5所示。
首先建立兩個固定坐標系OXYZ和O′X′Y′Z′，輸出軸轉動錐中心線取為軸OZ，輸入軸的軸線取為O′Z′，其中O與O′重為OZ與O′Z′交點，取軸OY與O′Y′重合，且垂直于形成夾角β的OZ和O′Z′兩軸所在平面，則坐標系O′X′Y′Z′可看作是坐標系OXYZ繞OY軸旋轉一個角度，即為輸入與輸出之間的夾角β所得。另外，在三叉桿上固連一動坐標系O″X″Y″Z″，原點O″即為三叉桿的交點，O″Z″即為實際輸出軸軸線，O″X″Y″平面即為三叉桿所在平面，且取軸O″Y″始終垂直于OX軸（即動坐標系O″X″Y″Z″也隨三叉桿作圓錐運動）。假定在初始狀態下，導向滑道軸線m1位于O′X′Z′平面內，三叉桿軸線n1位于與固定平面OXZ重合的動平面O″X″Z″內，當輸入軸轉過一角度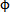
i時，輸出軸上三叉桿轉過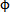o角,其中輸入軸轉過角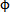i時，在坐標系O′X′Y′Z′中位置如圖3-4所示（圖3-4中右圖為左視圖，wi為輸入轉速），這樣建立坐標系后，就可以利用引入齊次坐標的方向余弦矩陣——四階變換矩陣進行運動方面的分析了。
3.2.4 運動分析
按圖3-5所示坐標系，可先在動坐標系O″X″Y″Z″中建立三叉桿軸頸的軸線參數方程然后通過坐標變換轉至固定坐標系O′X′Y′Z′中，因輸入軸的滑道軸線同三叉桿軸頸的軸線相交（于小桿球面的中心），故在坐標系O′X′Y′Z′中聯立三叉桿軸頸的軸線參數方程和輸入軸的滑道軸線參數方程，在這個聯立的方程中會出現兩個未知量即輸出轉角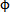o和動坐標系中的一個坐標x″，方程數和未知量數是相同的，可以求解，通過消除X″即可求得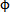i同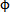o的關系；同時小桿球面的中心在固定坐標系O′X′Y′Z′中的運動軌跡也可求出。
上一頁
下一頁
