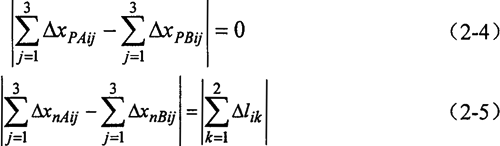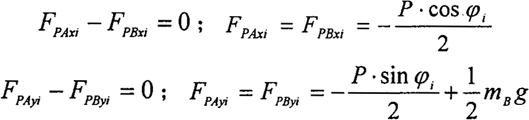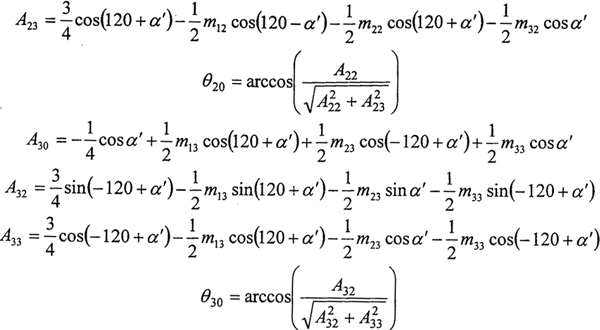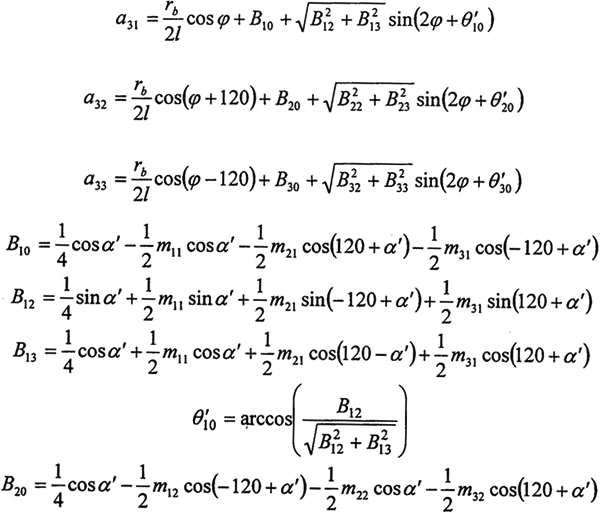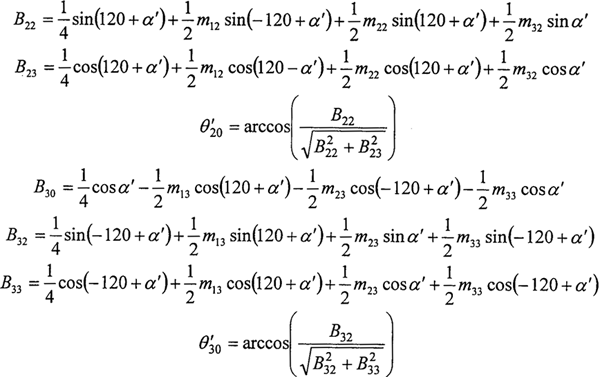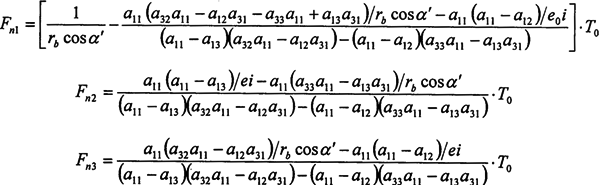第2章 完全平衡雙軸輸入三環減速器的動力學研究
2.1 引言
三環減速器的研究起步較晚,產品研制的時間較短,盡管一些廠家和科研院所對其進行過一些研究和試驗,取得了一些成果,但是,生產中出現的諸如:振動大、溫升高及轉臂軸承使用壽命短等諸多問題還未得到有效地解決,這嚴重影響了三環減速器的推廣使用。目前,三環減速器的受力分析、效率計算和振動及發熱等問題的研究表明,采用雙軸輸入及對稱型三環傳動形式可減少三環減速器的振動,進而提高三環減速器的使用壽命。受力分析是三環減速器設計的基礎,針對目前三環減速器變形協調條件處理過程簡單化、影響計算精度的問題,本章改進了考慮環板形狀和受力實際的變形協調條件,并對三環減速器的受力進行了分析;依據連桿機構平衡理論,提出了完全平衡雙軸輸入三環減速器設計的理論依據;曲柄軸和輸出軸的支撐軸承處的受力分析揭示出慣性力和慣性力矩、嚙合力對基本型和完全平衡型三環減速器振動的影響;最后,本章還對完全平衡三環減速器的振動問題進行了研究,結果表明:完全平衡雙軸輸入式三環減速器有著優越的機械性能。
2.2 基本型三環減速器的受力分析
2.2.1 結構組成及基本原理
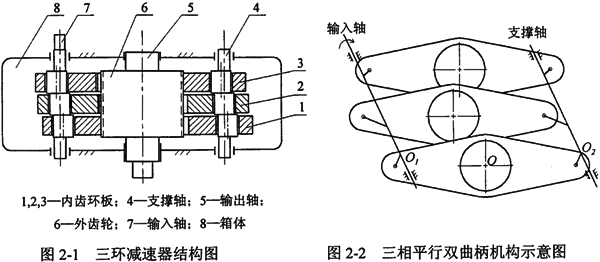
現有的理論研究、試驗分析和產品的應用都證明,對稱型三環減速器較偏置型有著優越的機械性能,作為筆者設計的完全平衡雙軸輸入式三環減速器的對比樣機,本章選的是對稱型三環減速器。對稱型三環減速器的基本結構如圖2-1所示,其輸入軸和支撐軸對稱布置在輸出軸的兩側。其輸入軸通過三片完全相同且互成120°的偏心套及相匹配的滾動軸承與內齒環板構成三個平行雙曲柄機構,傳動環板在輸入軸的驅動下作軌跡為圓的平動,傳動環板上的內齒圈與輸出軸上的外齒輪相嚙合,實現了輸出軸的低速輸出。每一片內齒環板均為一個平行雙曲柄機構,三塊環板同時驅動輸出軸齒輪。理論上,任一瞬時各環板所受的載荷大小相等,由于不可避免的制造安裝誤差及傳動過程中的彈性變形,使實際工作時各環板所受載荷并不相同,也就是各傳動環板之間的載荷分配不夠均勻。這種現象嚴重影響三環減速器性能的發揮,并產生振動和噪音,嚴重時,會導致異常工作情況甚至出現事故。現有三環減速器采用哪圖2-2所示三相平行雙曲柄機構的目的主要是克服機構死點和使慣性力平衡。
2.2.2 慣性力和慣性力矩
設內齒環板的質量為mB,轉臂偏心曲柄的質量(含轉臂軸承)為mH,環板的質心在O點,兩轉臂偏心軸的瞬時質心分別在O1,O2點,轉臂轉速為nH,因內齒環板作平動,則其轉速nb為零,因而,質心以nH轉速繞O1,O2轉動,rb2為內齒輪的基圓半徑,rb1為外齒輪的基圓半徑,α為壓力角,α′為嚙合角,e0為偏心距,m為內或外齒輪的模數,Z1,Z2為內嚙合的內、外齒輪的齒數。每片內齒環板的慣性力為:
Pi=mBωH2e0=[mπ2(Z2-Z1)m內/1800]·(cosα/cosα′)·nH2 (2-1)
每個轉臂偏心軸(曲柄)的慣性力為:
PHi=mHωH2e0=[mπ2(Z2-Z1)mH/1800]·(cosα/cosα′)·nH2 (2-2)
這里,i=1,2,3
2.2.3 三環減速器的變形協調條件
三環減速機運動屬靜不定問題,用一般平面剛體力學方法無法完全求出機構的作用力,影響到三環減速器設計和傳動性能的改進。為此需要考慮各構件的變形,建立能充分反映三環減速器實際受力的變形協調條件作為補充方程。三環減速機傳動機構是雙曲柄連桿機構,曲柄的旋轉半徑是偏心軸的偏心距,曲柄布置在由支撐軸承支承的偏心軸上,環板是雙曲柄機構的連桿,傳動過程中的主要變形有各構件的接觸變形、軸的扭轉彎曲變形、環板的拉壓變形等等。根據位移變形分析可知,軸的彎曲變形和環板的拉壓變形是主要的變形形式。對于筆者設計的如圖2-3所示的環板,設A為輸入軸,B為輸出軸。為了計算上的方便,以前將其簡化為等截面桿處理。實際上,由于有效截面的最大面積是最小截面面積的5倍多,這種簡單地處理和實際有較大的差別。環板受拉壓變形時的有效拉壓面積的形狀如圖2-4所示(單位:mm)。

其實際的拉壓截面曲線由下面的方程分段給出(長度單位:mm):

式中 A0=58.594; A1=0.36736; rk=42.5; r2=81.8; l=145
由方程繪出這際拉壓截面曲線圖可看出,工程上所用的實際環板的結構形狀和方程較為復雜,對其拉壓變形量難以直接積分求解。但簡單地將有效截面的最大面積與最小截面面積相差5倍的環板的有效拉壓面積處理成等截面圓柱則誤差較大。由于嚙合力連續作用在曲線方程較為復雜的中間各位置點,若根據實際形狀(方程)加以積分求解在數學上又較為困難。對于此類問題,采用工程上實用的最小二乘法將實際曲線擬合成分段斜直線組成的近似函數,則很有效,這樣做,既可保證精度,又可用簡單的積分公式編程直接求解。
盡管轉臂軸承兩端的截面尺寸也不大,但由于軸承外表面與環板接觸的斷面積較大,且軸承的剛度較大,故此處產生的擠壓變形與軸的彎曲變形相比較小,可忽略。
由于環板的結構是對稱的,對其中的1/4進行研究就可以了。根據環板的實際,將圖形分成10段。每段的擬合方程均為:
yi=A0i+A1ixi
每段方程中的系數如表2-1所示:
表2-1 方程的系數
| |
AB |
BC |
CD |
DE |
EF |
FG |
GH |
HI |
IJ |
JK |
| A0 |
16.09 |
15.43 |
11.96 |
-9.00 |
-251.97 |
58.86 |
365.5 |
130.3 |
68.95 |
34.36 |
| A1 |
0.43 |
0.56 |
0.86 |
1.65 |
5.19 |
0.36 |
-4.61 |
-1.13 |
-0.42 |
-0.083 |
設任一環板在x方向上分別受到FAix、FBix、嚙合力Fni,水平分力和慣性力Pi,水平分力的拉伸或壓縮作用;如圖2-5所示的輸入軸上任一環板兩環板支點Ai(Bi)在x方向的撓度△x為偏心軸頸上環板軸承x方向的作用力FA1x,FA2x,FA3x(FB1x,FB2x,FB3x)在Ai(Bi)點作用的撓度△xAi(Bi)的疊加。以S代表輸入軸支承軸承與相鄰環板之間的距離,d表示相鄰環板之間的距離。則考慮輸入軸的彎曲變形和環板拉壓變形三環減速機變形協調條件為:在外力作用下,任一環板處兩曲柄軸在x方向的撓度的差等于該環板在x方向的總變形。用公式2-3表示。


實際運算中,采用下面的形式更為有效,求解也更為方便。(2-4)式的證明將在下一節的受力分析中給出證明。
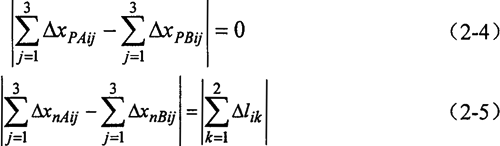
式中 △xAij,△xPAij,△xnAij,——在一輸入軸上環板處Ai點的由于力FAjx,FPAjx,FnAjx作用的撓度(j=1,2,3);這里,FAjx=FPAjx+FnAjx。
△xBij, △xPBij,△xnBij——另一輸入軸上環板處Bi點的由于力FBjx,FPBjx,FnBjx作用的撓度(j=1,2,3);這里FBjx=FPBjx+FnBjx。
△lik——對應于AiBi的一塊環板在x方向由嚙合力水平分力作用下產生的拉壓變形(k=1,2)。
2.2.4 三環減速器的受力分析
1.轉臂軸承上的作用力分析 內齒環板受力見圖2-6所示。
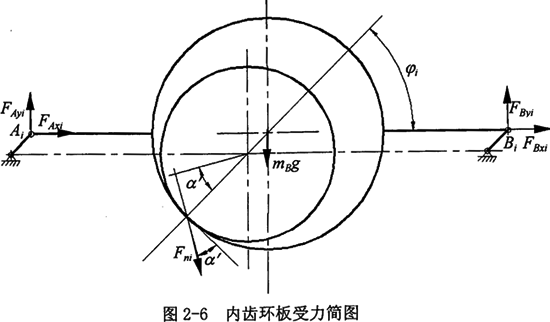
設兩轉臂偏心軸的瞬時幾何中心分別在A和B點,L0為內齒環板中心與轉臂軸承中心之間的距離,Fn為外齒輪作用給內齒板的力(切于基圓,指向嚙合點)。轉臂軸承上Ai和Bi的作用力為FAi(分解為FAxi和FAyi)和FBi(分解為FBxi和FByi),由力(力矩)平衡方程,對于第i塊環板可列如下方程:

由于方程數為12個,而方程中的未知量的總數為15個,屬靜不定問題。需建立變形協調方程作為補充方程,方程才能得以求解。
對于作用在任意一塊環板的慣性力和嚙合力來說,可根據力的疊加原理,將慣性力和嚙合力分別作用在Ai和Bi的力求出后,再將其疊加便可得到環板點Ai和Bi的作用力。由力學原理和變形協調方程有:
僅考慮環板上作用的慣性力和重力。
第i塊環板可列如下方程:
∑FPxi=FPAxi+FPBxi+Picosφi=0 (2-12)
∑FPyi=FPAyi+FPByi+Pisinφi-mBg=0 (2-13)
∑MPzi=FPByi·L0-FPAyi·L0=0 (2-14)
變形協調條件方程(假設環板的變形之和不為零):
|C1(FPAx1-FPBx1)+C2(FPAx2-FPBx2)+C3(FPAx3-FPBx3)|=|FPAx1C5-FPBx1C6| (2-15)
|C2(FPAx1-FPBx1)+C4(FPAx2-FPBx2)+C2(FPAx3-FPBx3)|=|FPAx2C5-FPBx2C6| (2-16)
|C3(FPAx1-FPBx1)+C2(FPAx2-FPBx2)+C1(FPAx3-FPBx3)|=|FPAx3C5-FPBx3C6| (2-17)
由于環板的慣性力作用在環板的中心,而環板的結構又是對稱的,故有C5=C6,代入上面方程并求解有:
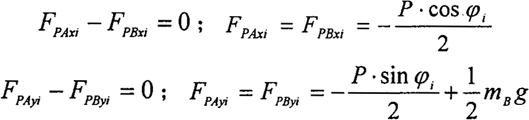
由于上式和C5=C6知,慣性力作用在環板上的拉壓變形之和為零,方程(2-4)式得證。
僅考慮環板上作用的嚙合力。
∑Fnxi=FnAxi+FnBxi-Fni·sin(φi-α′)=0 (2-18)
∑Fnyi=FnAyi+FnByi-Fni·cos(φi-α′)=0 (2-19)
∑Fnzi=FnAyi·L0-FnByi·L0-Fnirb=0 (2-20)
變形協調條件方程:
|C1(FnAx1-FnBx1)+C2(FnAx2-FnBx2)+C3(FnAx3-FnBx3)|=|FnAx1C5-FnBx1C6| (2-21)
|C2(FnAx1-FnBx1)+C4(FnAx2-FnBx2)+C2(FnAx3-FnBx3)|=|FnAx2C5-FnBx2C6| (2-22)
|C3(FnAx1-FnBx1)+C2(FnAx2-FnBx2)+C1(FnAx3-FnBx3)|=|FnAx3C5-FnBx3C6| (2-23)
式中

式中 E——環板材料的彈性模量,本文取為2.06×1011N/m2;
I——軸的截面對中性軸的慣矩,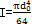 。
。
xF=l-rcosφi
將FnBxi=-FnAxi+Fnxi代入式(2-21)~(2-23)中,求解得:
FnAX1=m11Fn1x+m12Fn2x+m13Fn3x
FnAX2=m21Fn1x+m22Fn2x+m23Fn3x
FnAX3=m31Fn1x+m32Fn2x+m33Fn3x
式中

由此可得到各個環板轉臂軸承所受的力。

將以上關系代入支撐軸方程(2-9),并整理有:
a11Fn1+a12Fn2+a13Fn3=0 (2-24)
式中

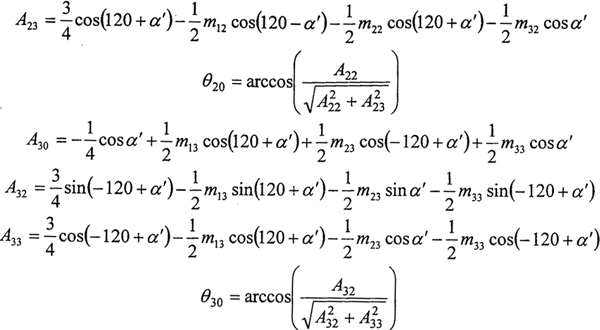
代入輸入軸方程(2-11),并整理有:
a31Fn1+a32Fn2+a33Fn3=Tr/e0 (2-25)
式中
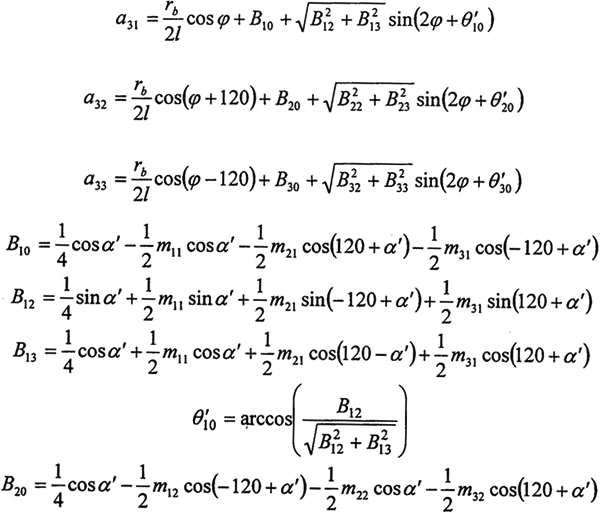
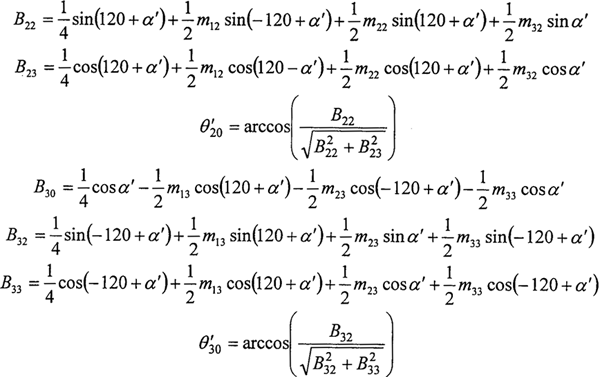
求解曲柄軸(2-24)、(2-25)和輸出軸(2-10)組成的關于嚙合力的方程組,可解得:
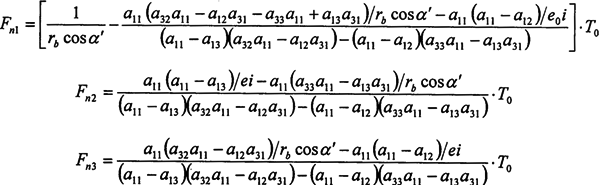
由上式可看出,任意時刻各環板上作用的嚙合力是不相等的,且是與轉角、環板和曲柄軸結構尺寸、壓力角以及偏心尺寸有關的復雜函數,假設各嚙合力相等或者是成一簡單的函數關系都是與實際嚴格不符的。若需要用簡潔的函數關系加以描述,應首先利用上式求出輸出軸旋轉一周時的數個嚙合力的表達式,這里不作詳細的討論。
上一頁
下一頁