第三章 彈性共軛曲面原理的應(yīng)用研究
3.1 彈性共軛曲面原理的基本問題
由第二章可知,解決彈性共軛曲面,涉及到變形基本曲面Σ1d和Σ2d、嚙合軌跡圖形Σc、彈性共軛曲面Σ1和Σ2、運動參數(shù)V1和V2、曲面的變形dr1(1)和dr2(2),而變形又與Σ1d、Σ2d及作用力有關(guān),這是一個非常復(fù)雜的多因素問題,尤其當(dāng)運動的自由度較大時,問題變得更為復(fù)雜。就變形基本曲面Σ1d和Σ2d、嚙合軌跡圖形Σc、運動參數(shù)V1和V2這五個因素而言,存在著如第一章所論述的五類基本問題。由于彈性共軛曲面問題還包含彈性共軛曲面Σ1、Σ2和曲面變形的因素,因此,需求解的內(nèi)容更為豐富。本文只討論已知變形基本曲面Σ1d及外力,求給定運動規(guī)律下的兩彈性共軛曲面,此類問題主要解決嚙合傳動問題。
3.2 平面嚙合傳動彈性共軛曲面的求解
定軸平面嚙合傳動坐標(biāo)系如圖3-1所示。

3.2.1 變形基本曲面
在定軸平面嚙合中,不考慮軸系的變形,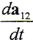 =0,由(2-7-1)式得
=0,由(2-7-1)式得

若在變形狀態(tài)下Σ1d為已知,則可求得與之共軛的變形基本曲面Σ2d。若將(3-2-1)式表示為
f(u,φ1)=0
式中 u——曲面參變量,φ1——Σ1d的轉(zhuǎn)角,則有

式中 M21——S1、S2坐標(biāo)系轉(zhuǎn)換矩陣
3.2.2 最大變形是關(guān)于載荷大小和作用位置的函數(shù)
δ(p,u)=δp(p,u)+δb(p,u) (3-2-3)
式中 p——載荷參變量
δ(p,u)——總變形矢量
δp(p,u)——接觸變形矢量
δb(p,u)——撓曲變形矢量
通常所求得的變形為數(shù)值解。
3.2.3 求解彈性共軛曲面

3.2.4 漸開線直齒圓柱標(biāo)準(zhǔn)齒輪傳動彈性共軛曲面的求解
1.變形基本曲面
坐標(biāo)系如圖3-1所示。設(shè)已知齒輪1的變形基本曲面為漸開線曲面,其端面上的齒面線方程為

式中 u——曲面參變量
rb1——齒輪1漸開線基圓半徑
則


a12=a12i
將rd(1)、ω(1)、ω(2)、a12代入(3-2-1)式,有

化簡后得
cos(u-φ1)=rb1/r1=cosα
α為齒輪的分度圓壓力角,所以
α=u-φ1
由(3-2-2)式,得

代入并化簡得:

顯然Σ2d齒廓曲線也是一漸開線,其基圓半徑與i21有關(guān),漸開線起點不在x2軸線上。
2.變形的求解
對于直齒圓柱齒輪變形的求解,已有許多研究[33][46][49][50][54~56][60~62]。文獻[49]較好地解決了撓曲變形的問題,提出的變形計算的擬合公式簡捷、精度高;文獻[46]對接觸變形問題根據(jù)經(jīng)典的赫茲公式,推導(dǎo)出直齒圓柱齒輪的接觸變形計算公式,計算簡便,精度高,本節(jié)擬采用上述兩公式進行變形計算。
撓曲變形:

其中A、B、C按以下三式計算

當(dāng)z<25時取“+”號;當(dāng)z≥25時取“-”號。
(3-2-4)式中
E——材料彈性模量(kg/mm2)
Pn——作用在齒面上的法向總載荷(kg)
b——齒寬(mm)
z——齒數(shù),z取17~∞,當(dāng)z>135時,按z=135計算
xr——徑向變位系數(shù),xr取值-0.2~1.0
λ——加載點位置系數(shù),λ=(ra-rk)/m,ra為齒頂圓半徑,rk為加載點半徑,m為齒輪模數(shù)
δb——輪齒加載點法向撓曲變形量
(3-2-4)式適合于齒輪材料泊輪比為0.3,無根切無齒頂變尖的直齒圓柱齒輪的撓曲變形的計算。刀具齒條齒形角α=20°,齒頂高系數(shù)ha*=1,頂隙系數(shù)c*=0.25,刀尖圓角半徑r0允許在0.25m~0.4m范圍變化。
接觸變形:

式中
Pn——作用在齒面上的法向總載荷(kg)
E——材料彈性模量(kg/mm2)
v——材料泊松比
b——齒寬(mm)
m——齒輪模數(shù)(mm)
a——赫茲接觸寬度的一半(mm)
δp——輪齒加載點接觸變形量
對于柱體的接觸變形,文獻[112][113]介紹了赫茲接觸半寬度的計算公式

式中
P——單位接觸長度上的載荷(kg/mm)
R1、R2——兩接觸體在接觸點的曲率半徑(mm)
v1、v2——材料的泊松比
E1、E2——材料的彈性模量(kg/mm2)
當(dāng)兩接觸體材料相同時

計算變形所需幾何尺寸的確定:
模數(shù)m,齒數(shù)z1、z2,壓力角α,變位系數(shù)xr1=0、xr2=0,齒寬b,齒頂高系ha*,頂隙系數(shù)c*,齒頂圓半徑ra1=mz1/2+mha*,齒根圓半徑rf1=mz1/2-m(ha*+c*),齒輪1加載點半徑r1k變化范圍設(shè)為 ,曲率半徑為
,曲率半徑為

法向作用力:
設(shè)已知作用在齒輪1上的轉(zhuǎn)矩為M,則無論接觸點在何處,有
Pn=M/rb1
由變形基本曲面的求解得,Σ1d、Σ2d為基圓半徑分別為rb1、rb2的漸開線曲面;將以上各已知參數(shù)代入(3-2-4)及(3-2-5)式,在r1k取值范圍內(nèi)以一定間隔取若干值分別計算變形,得到兩齒面以r1k為參數(shù)的變形量離散值,為了求解以u為參變量的彈性共軛曲面,需將其換算為以u為參數(shù)的變形量,由r1k與u的關(guān)系 ,即可得到以u為參變量的變形量離散值δ(1)(u)=δp(1)(u)+δb(1)(u)、δ(2)(u)=δp(2)(u)+δb(2)(u)
,即可得到以u為參變量的變形量離散值δ(1)(u)=δp(1)(u)+δb(1)(u)、δ(2)(u)=δp(2)(u)+δb(2)(u)
變形基本曲面單位法向量的分量為
n(1)xd0=sinu,n(1)yd0=-cosu。
3.彈性共軛曲面求解
齒輪1的彈性共軛曲面為
x(1)(u)=xd(1)(u)+δ(1)(u)sinu
y(1)(u)=yd(1)(u)-δ(1)(u)cosu
同理可求得
x(2)(u)=xd(2)(u)+δ(2)(u)sinu
y(2)(u)=yd(2)(u)-δ(2)(u)cosu
下面以m=3mm,z1=29,z2=50,α=20°,ha*=1,c*=0.25,b=30mm,xr1=xr2=0為例求解彈性共軛曲面,設(shè)v=0.3,E=2.1×104kg/mm2,M=500.0Nm。
本例彈性共軛曲面計算結(jié)果如表3-1所給。為計算方便,設(shè)齒面2漸開線起點在x2上。
表3-1 變形基本曲面坐標(biāo)及彈性共軛曲面坐標(biāo)
(m=3mm,z1=29,z2=50,α=20°,ha*=1,c*=0.25,b=30mm,xr1=xr2=0,v=0.3,E=2.1×104kg/mm2,M=50.0kgm)
| u1 |
xd(1) |
x(1) |
yd(1) |
y(1) |
u1 |
xd(1) |
x(1) |
yd(1) |
y(1) |
| 0.059942 |
40.9500 |
40.9514 |
0.0029 |
-0.0200 |
0.238276 |
72.4493 |
72.4541 |
0.3160 |
0.2964 |
| 0.147685 |
41.3200 |
41.3232 |
0.0438 |
0.0221 |
0.259993 |
72.8188 |
72.8241 |
0.4101 |
0.3904 |
| 0.200480 |
41.6899 |
41.6942 |
0.1094 |
0.0879 |
0.280131 |
73.1882 |
73.1939 |
0.5124 |
0.4924 |
| 0.242359 |
42.0596 |
42.0648 |
0.1928 |
0.1715 |
0.299006 |
73.5574 |
73.5636 |
0.6224 |
0.6022 |
| 0.278293 |
42.4290 |
42.4351 |
0.2914 |
0.2700 |
0.316846 |
73.9263 |
73.9330 |
0.7398 |
0.7193 |
| 0.310355 |
42.7981 |
42.8050 |
0.4034 |
0.3818 |
0.333816 |
74.2950 |
74.3022 |
0.8642 |
0.8433 |
| 0.339643 |
43.1668 |
43.1745 |
0.5277 |
0.5059 |
0.350044 |
74.6634 |
74.6712 |
0.9953 |
0.9740 |
| 0.366821 |
43.5349 |
43.5435 |
0.6635 |
0.6414 |
0.365626 |
75.0314 |
75.0398 |
1.1330 |
1.1111 |
| 0.392330 |
43.9025 |
43.9119 |
0.8102 |
0.7876 |
0.380644 |
75.3992 |
75.4082 |
1.2770 |
1.2545 |
| 0.416475 |
44.2694 |
44.2797 |
0.9673 |
0.9442 |
0.395161 |
75.7666 |
75.7762 |
1.4271 |
1.4039 |
| 0.439481 |
44.6356 |
44.6468 |
1.1344 |
1.1106 |
0.409231 |
76.1335 |
76.1440 |
1.5832 |
1.5591 |
| 0.461519 |
45.0009 |
45.0131 |
1.3111 |
1.2865 |
0.422898 |
76.5001 |
76.5114 |
1.7452 |
1.7200 |
| 0.482722 |
45.3653 |
45.3787 |
1.4972 |
1.4716 |
0.436200 |
76.8662 |
76.8785 |
1.9129 |
1.8865 |
| 0.503194 |
45.7287 |
45.7435 |
1.6925 |
1.6655 |
0.449169 |
77.2318 |
77.2454 |
2.0863 |
2.0582 |
| 0.523022 |
46.0910 |
46.1075 |
1.8967 |
1.8680 |
0.461834 |
77.5969 |
77.6119 |
2.2651 |
2.2350 |
| 0.542277 |
46.4521 |
46.4707 |
2.1096 |
2.0787 |
0.474220 |
77.9615 |
77.9783 |
2.4494 |
2.4167 |
3.3 空間嚙合傳動彈性共軛曲面的求解
3.3.1 變形基本曲面的求解
由變形基本曲面運動基本方程(2-7-1)及已知的一個變形基本曲面,可求得另一變形基本軛曲面。

式中u、v為曲面參變量,f(u,v,φ1)=0為(2-7-1)式的參數(shù)表達式。
3.3.2 變形的求解
空間嚙合時,變形基本曲面上每一瞬時的接觸線方程可以求出,在某一瞬時的接觸線上各點的變形便可以求出。整個齒面各點的變形就是所有接觸線變形的集合。
S={δ|δ={δ所有接觸線}}
空間嚙合時,接觸線上各點彈性變形的求解是三維彈性接觸問題的變形求解,目前較多的是采用有限元或邊界元方法,這方面已有一些研究[78],但仍缺乏較成功的計算軟件。由于三維彈性接觸問題變形的求解涉及的因素較復(fù)雜,一般很難給出變形計算的擬合公式,某些空間嚙合傳動(如斜齒圓柱齒輪傳動)雖可以得出變形計算擬合公式[54],但擬合公式仍較復(fù)雜,且計算精度較低。隨著三維彈性接觸問題變形求解研究的發(fā)展,將進一步提高彈性共軛曲面求解的精度。
3.3.3 彈性共軛曲面的求解
r(i)(u,v)=rd(i)(u,v)+δ(i)(u,v) (i=1,2)
其中 δ(u,v)=δp(u,v)+δb(u,v)
δp(u,v)為接觸變形矢量,δb(u,v)為法向撓曲變形矢量。
彈性共軛曲面Σi就是各離散點r(i)(u,v)的集合。

3.3.4 鼓形齒聯(lián)軸器彈性共軛齒面求解方法
共軛齒面鼓形齒聯(lián)軸器由漸開線直齒圓柱內(nèi)齒輪和與之共軛的相同齒數(shù)的外齒輪組成。內(nèi)外齒輪軸線有一軸間傾角θ,其傳動原理如圖1-2所示。以下根據(jù)空間嚙合彈性共軛曲面的求解方法,討論在已知作用轉(zhuǎn)矩下的內(nèi)外齒輪彈性共軛齒面求解方法。
3.3.4.1 變形基本曲面
1.坐標(biāo)系(如圖3-2所示)

S1(o,x1,y1,z1)坐標(biāo)系,為與外齒輪固連的動坐標(biāo)系;z1軸與外齒輪軸線重合。
S10(o,x10,y10,z10)坐標(biāo)系,為過渡坐標(biāo)系;z10與z1軸重合;x10與x1夾角φ1為某瞬時外齒輪轉(zhuǎn)角。當(dāng)φ1=0時,S10系與S1系重合。
S2(o,x2,y2,z2)坐標(biāo)系,為與內(nèi)齒輪固連的動坐標(biāo)系;x2為某一齒槽和齒寬中線;z2軸與內(nèi)齒輪軸線重合。
S20(o,x20,y20,z20)坐標(biāo)系,為靜坐標(biāo)系;z20軸與z2軸重合;x20軸與x2軸夾角φ2為某瞬時內(nèi)齒輪轉(zhuǎn)角,φ2=0時,S20系與S2系重合。
四個坐標(biāo)系有共同的原點O,x10與x20軸線重合,z10與z20軸線夾角為兩齒輪軸線的軸交角θ(y10與y20軸線夾角亦為θ)。
2.坐標(biāo)轉(zhuǎn)換關(guān)系

坐標(biāo)的逆變換可由它們的逆矩陣導(dǎo)出。
3.內(nèi)齒輪變形基本曲面方程
設(shè)內(nèi)齒輪變形基本曲面為漸開線曲面,其端面上的齒面線及坐標(biāo)如圖3-3所示。

xc2軸通過漸開線在基圓上的起點。(o,xc2,yc2,zc2)坐標(biāo)系下的曲面方程為

式中 ψ2、t2——曲面參變量;rb——漸開線基圓半徑。設(shè)α2為曲面某一點K處的壓力角,則有ψ2=tgα2。將(3-3-2)式轉(zhuǎn)換到S20坐標(biāo)系,方程為

式中λ2=ψ2-β2+φ2
β2——內(nèi)齒輪基圓齒槽寬所對圓心角之半。
β2=π/(2z)+(2xr2tgα+xτ2)/z+tgα-α
式中 xr2——徑向變位系數(shù)
xτ2——切向變位系數(shù)
(3-4-2)式就是在S20系的內(nèi)齒輪變形基本曲面方程。
4.外齒輪變形基本曲面方程
由 n·[(ω(2)-ω(1))×rd(2)]+n·(ω(1)×a12)-n·da12/dt=0,不計軸系的變形,da12/dt=0,相交軸傳動a12=0,有
n·[(ω(2)-ω(1))×rd(2)]=0 (3-3-4)

所以 n=rbψ2(sinλ2i20-cosλ2j20)
令|ω(2)|=|ω(1)|=1,則ω(2)=k20,ω(1)=-sinθj20+cosθk20。

將n、ω(2)、ω(1)、rd(2)代入(3-3-4)式,得

化簡得
t2sinλ2sinθ-rb(1-cosθ)=0 (3-3-5)
(3-3-5)式就是本問題的彈性共軛曲面運動基本方程,它是關(guān)于t2、ψ2、φ2的函數(shù),可表示為f(t2,ψ2,φ2)=0
外齒輪變形基本曲面方程r1d(1)為

令φ1=φ2=φ,將M1,2、r2d(2)及f(t2,ψ2,φ2)=0解出的φ代入(3-3-6)的第三式,則可得到以t2、ψ2為參變量的外齒輪曲面的表達式。

其中 t2=rb(1-cosθ)/[sin(ψ2-β2+φ)sinθ]
為了求解變形,還需求得內(nèi)齒輪輪齒另一齒面的變形基本曲面方程,如圖3-4所示。

(o,xc2,yc2,zc2)坐標(biāo)系下的曲面方程為

用與前述相同的方法可求得以t2、ψ2為參變量的外齒輪輪齒另一齒面的變形基本曲面方程為

其中 t2=rb(cosθ-1)/[sin(ψ2-β2+φ)sinθ]
3.3.4.2 求解變形
本文簡要介紹采用邊界元法求解鼓形齒聯(lián)軸器內(nèi)外齒輪輪齒變形的方法。
1.三維彈性問題邊界元法的基本理論[114][115]
三維彈性問題邊界元法是根據(jù)線彈性力學(xué)的基本方程及邊界條件和虛功互等定理或加權(quán)余量概念,導(dǎo)出邊界積分方程,再將邊界積分方程離散,把所解問題定義域的邊界劃分為若干單元,然后在每個單元上利用插值公式把邊界未知量表示成依賴于節(jié)點未知量的函數(shù)。對于三維域上定解問題而言,需離散的區(qū)域僅為二維的邊界面。對于邊界上每個節(jié)點建立線性代數(shù)方程,形成一代數(shù)方程組。求解這個方程組,即可解得各節(jié)點的未知位移和應(yīng)力值。三維彈性接觸問題的邊界元法[78],是運用三維彈性問題邊界元法,以接觸體為研究對象,考慮光滑條件、平衡條件、位移協(xié)調(diào)條件和單側(cè)條件等接觸邊界條件,求解接觸問題的結(jié)點未知位移和應(yīng)力值。其求解過程,必須首先給定初始接觸區(qū),再根據(jù)計算判斷接觸區(qū)是否滿足接觸區(qū)判定準(zhǔn)則,若不滿足,再進行接觸區(qū)調(diào)整,直到滿足接觸區(qū)判定準(zhǔn)則,即可求得各節(jié)點的未知位移和應(yīng)力值。
2.邊界元模型
本論文不討論三維彈性接觸問題的求解方法,著重于應(yīng)用三維彈性接觸問題邊界元法來求解鼓形齒聯(lián)軸器內(nèi)外齒輪齒面的彈性共軛曲面。為了求解變形基本曲面的變形,首先要確定其數(shù)值模型,進行單元的劃分。
設(shè)內(nèi)齒輪為主動輪,將一輪齒從左右齒槽中點到輪體外圓以軸截面取出,如圖3-5所示。在輪體截取面上作用均布力,其約束為繞齒輪軸線轉(zhuǎn)動而不能有軸向位移。外齒為從動輪,將一輪齒從左右齒槽中點到齒輪內(nèi)孔以平行于輪齒中線和齒輪軸線的平面取出,如圖3-6所示。截面上的面力為未知,其約束為各方向位移為零。

以上的輪齒邊界元模型與實際的約束和加載情況較接近。當(dāng)計算精度有更高要求時,可適當(dāng)擴大取出體范圍。顯然,擴大的模型必須劃分更多的單元,計算量更大。
接觸問題的邊界單元劃分有其特殊的要求,一般對于非接觸區(qū)域根據(jù)精度要求劃分較大單元。由于接觸的可能區(qū)域在接觸線附近,因此,需在接觸線附近適當(dāng)劃分較小的單元,以滿足計算中接觸區(qū)域的調(diào)整,求得較精確的變形值。
3.3.4.3 彈性共軛曲面
設(shè)在齒面某一點rd(i)的法向變形為δ(i),則該點的彈性共軛曲面數(shù)值解為
r(i)=rd(i)+δ(i)n0(i)
式中n0(i)為齒面的外法線單位矢量。
整個齒面的彈性共軛曲面為所有數(shù)值解的集合
Σ={r|r={r(i)全體齒面點}}
3.4 多齒嚙合的彈性共軛曲面
前面我們所討論的是兩彈性體單對曲面連續(xù)接觸運動的彈性共軛曲面問題的求解,它是彈性共軛曲面問題求解的基礎(chǔ)。在工程實際中,大量地存在兩彈性體有多對曲面同時接觸運動,且同時接觸的曲面對數(shù)有規(guī)律地變化,如切削加工的多刀刃切削和齒輪傳動中的多齒嚙合等等。由于彈性體多對曲面接觸時的載荷分配與曲面的幾何特征相互作用及多對曲面接觸的數(shù)目變化的過渡,它與在剛性條件下的共軛曲面與共軛運動的關(guān)系不同。研究在彈性條件下,多對共軛曲面與共軛運動的關(guān)系,有重要的理論和現(xiàn)實意義。本節(jié)以齒輪傳動為例,討論彈性體多對齒面嚙合的彈性共軛曲面問題。
3.4.1 坐標(biāo)系及齒面
坐標(biāo)系及齒面如圖3-7所示。
坐標(biāo)系S1(o1,x1,y1,z1):與輪1固連的動坐標(biāo)系;
坐標(biāo)系S2(o2,x2,y2,z2):與輪2固連的動坐標(biāo)系;
坐標(biāo)系S(o,x,y,z):靜坐標(biāo)系;
坐標(biāo)系S20(o2,x20,y20,z20):過渡坐標(biāo)系。
設(shè)當(dāng)前同時有n對齒嚙合,k1、k2…kn為各齒對接觸參考點。rl(m,n)表示在l坐標(biāo)下齒輪m的第n對齒的接觸參考點徑矢。

3.4.2 各齒對相對運動
由第二章分析知,某一齒對的相對運動為

式中 vi(12)——第i對齒面相對運動速度矢量
ωi(1)ωi(2)——齒輪1、齒輪2上第i對齒面的角速度矢量
不考慮軸系的變形,有

將(3-4-2)、(3-4-3)、式代入(3-4-1)式,得

 分別為兩齒輪第i對齒面參考點相對于S1、S2坐標(biāo)系的彈性變形速度矢量。
分別為兩齒輪第i對齒面參考點相對于S1、S2坐標(biāo)系的彈性變形速度矢量。
3.4.3 多齒對彈性共軛曲面運動基本方程
根據(jù)彈性共軛曲面基本概念,有
ni·vi(12)=0
即

在不同的多齒嚙合狀態(tài),運用(3-4-5)式,有不同的參數(shù)間的影響情況,以下將多齒嚙合狀態(tài)分為多齒接觸對數(shù)穩(wěn)定狀態(tài)和多齒接觸對數(shù)變化過渡狀態(tài)兩種情況分別討論。
3.4.4 多齒接觸對數(shù)穩(wěn)定狀態(tài)的彈性共軛曲面
3.4.4.1 多齒接觸對數(shù)穩(wěn)定狀態(tài),各接觸齒對的參考點在該狀態(tài)任一瞬時各齒對都處于最大變形狀態(tài),不存在變形開始的初期階段和變形的恢復(fù)階段。因此,在這個階段,各接觸齒面參考點都處于變形已結(jié)束,回彈尚未開始的狀態(tài)。很顯然,在此狀態(tài)有

另一方面,該狀態(tài)下的任一瞬時,兩齒面參考點的運動應(yīng)與各自齒輪的運動相吻合,否則與前述要求矛盾,因此有

綜合以上分析,將(3-4-6)、(3-4-7)式代入(3-4-5)式有

式中 rd(1,i)為接觸參考點在最大變形狀態(tài)的徑矢。
(3-4-8)式就是多齒接觸對數(shù)穩(wěn)定狀態(tài)的彈性共軛曲面嚙合基本方程。
3.4.4.2 多齒接觸對數(shù)穩(wěn)定狀態(tài)的彈性共軛曲面求解
由(3-4-8)式知,它與單對齒嚙合的彈性共軛曲面的求解類似。但由于它是多對齒同時嚙合,嚙合齒對的變形求解與每對齒的承受的載荷有關(guān),因此變形的計算要復(fù)雜得多。
1.變形基本曲面的求解
變形基本曲面為在變形最大情況下由彈性共軛嚙合點構(gòu)成,它是在整個嚙合過程中逐漸形成的動態(tài)曲面。設(shè)rd(1,i)已知,則由齒輪輪齒在輪體上的等分性,Σd(1,i-1)、Σd(1,i+1)為在Σd(1,i)前后相差一個齒距角的位置上,因此不難給出rd(1,1)、rd(1,2)、…rd(1,n)的方程。
不妨將(3-4-8)式寫成如下形式
f(u,v,φ1)=0 (3-4-8a)
式中u、v為曲面參變量,φ1為運動參數(shù)。
根據(jù)共軛曲面求解方法,可求得與rd(1,i)(i=1,2,…,n)共軛的變形基本曲面rd(2,i)(i=1,2,…,n)。

2.變形的求解
由三維彈性接觸問題的邊界元法可以求出各共軛接觸點的最大變形。但這是一個非連續(xù)多區(qū)域接觸問題,從理論上講,它可能發(fā)生接觸的邊界Γck分別為Γc(k,1)、Γc(k,2)、…、Γc(k,n),它們分別滿足滑動邊界和自由邊界的條件。確定適當(dāng)?shù)臄?shù)值模型及邊界積分方程的離散,同樣可以算出各自的變形。顯然多齒嚙合狀態(tài)的邊界元模型較單對齒嚙合要復(fù)雜得多,尤其當(dāng)嚙合齒對較多時,模型更為復(fù)雜。這種情況的三維彈性接觸問題的邊界元方法尚未見有文獻報道,相信隨著邊界元方法的發(fā)展,這個問題將能得到解決。
整個多齒接觸對數(shù)穩(wěn)定狀態(tài)的彈性共軛曲面的變形的計算,不需要象單對齒嚙合那樣徑歷整個嚙合過程,因為根據(jù)彈性共軛點的一一對應(yīng)性,某一對齒在某一位置的嚙合狀況與另外任一齒在該位置的嚙合狀況是一致的。因此只要將n對同時嚙合的齒對的嚙合狀況的并集作為整個多齒接觸對數(shù)穩(wěn)定狀態(tài)全過程,就可以以并集的方式得到這個過程中整個曲面的變形解。
3.彈性共軛曲面
設(shè)變形基本曲面上一點rj(k,i)=rdj(k,i)+δj(k,i)·n0j(k,i)
式中n0j(k,i)為曲面外法線單位矢量。
整個齒面的彈性共軛曲面為所有數(shù)值坐標(biāo)的集合
r={rj|j為所有多齒接觸對數(shù)穩(wěn)定狀態(tài)區(qū)間齒面點}
值得指出的是,當(dāng)多齒接觸對數(shù)n不同,雖然都是處于多齒接觸對數(shù)穩(wěn)定狀態(tài),但由于承擔(dān)載荷的齒對數(shù)不同,其變形也不同。因此,應(yīng)該對n不同的區(qū)域分別求解。
3.4.5 多齒接觸對數(shù)變化過渡狀態(tài)的彈性共軛曲面
若齒輪傳動形式所確定的彈性條件下多齒接觸對數(shù)為已知,設(shè)此數(shù)目為m和n。則嚙合過程中必然經(jīng)歷m對齒嚙合→n對齒嚙合和n對齒嚙合→m對齒嚙合這樣的過渡狀態(tài)。設(shè)m<n,則前一種情況就是有齒對嚙入而無齒對嚙出,后一種情況就是有齒對嚙出而無齒對嚙入。無論在哪一種過渡狀態(tài)都存在變形的不穩(wěn)定狀態(tài),嚙入的過程中,嚙入齒對經(jīng)歷了從無變形到最大變形的變形初始階段,嚙出齒對經(jīng)歷了從最大變形到無變形的變形恢復(fù)階段。
3.4.5.1 過渡狀態(tài)的彈性共軛曲面嚙合基本方程
在過渡狀態(tài)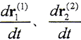 都不為零,因此對嚙入和嚙出齒面,嚙合基本方程為
都不為零,因此對嚙入和嚙出齒面,嚙合基本方程為

3.4.5.2 過渡狀態(tài)彈性共軛曲面分析
1.嚙入過程
在嚙入過程中,嚙入齒面經(jīng)歷了從無變形到最大變形的過程。在嚙入的最初瞬時,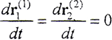 ,(3-4-10)式成為
,(3-4-10)式成為

(3-4-11)的形式與(3-4-8)的形式相同,但由于所處的受力變形狀態(tài)不同,二者是有差別的。(3-4-8)式的曲面參考點徑矢為rd,它表示處于最大變形狀態(tài)下的參考點徑矢,該點的彈性共軛曲面點為rd+δ·n0。而(3-4-11)式的曲面參考點徑矢r,它表示處于無變形狀態(tài)下的參考點徑矢,即它就是該瞬時的彈性共軛點。很顯然,嚙入瞬時的共軛接觸點少了δ·n0一項。通常嚙入過程從主動輪齒根與從動輪齒頂接觸開始,傳統(tǒng)的齒廓修形方法認(rèn)為應(yīng)該在齒頂和齒根修形。這里從彈性共軛曲面理論方面定性地證明了傳統(tǒng)的齒廓修形位置的正確性。
2.嚙出過程
在嚙出過程中,嚙出齒面經(jīng)歷了從最大變形到無變形的變形恢復(fù)過程,其過程為嚙入過程的逆過程,其機理與嚙入過程相似。當(dāng)嚙出齒對運動到主動輪和被動輪的齒距不等于變形基本齒面的節(jié)距位置,嚙合過程就開始了。在變形的恢復(fù)開始瞬時,仍處于變形最大的嚙合齒對的彈性共軛曲面要根據(jù)當(dāng)前瞬時的載荷分配進行計算,這與嚙入的情況是相同的。在嚙出的最后一刻,由于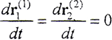 ,此時的情況與嚙入的最初瞬時相同。
,此時的情況與嚙入的最初瞬時相同。
上一頁
下一頁


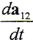 =0,由(2-7-1)式得
=0,由(2-7-1)式得













 ,曲率半徑為
,曲率半徑為 
 ,即可得到以u為參變量的變形量離散值δ(1)(u)=δp(1)(u)+δb(1)(u)、δ(2)(u)=δp(2)(u)+δb(2)(u)
,即可得到以u為參變量的變形量離散值δ(1)(u)=δp(1)(u)+δb(1)(u)、δ(2)(u)=δp(2)(u)+δb(2)(u)



















 分別為兩齒輪第i對齒面參考點相對于S1、S2坐標(biāo)系的彈性變形速度矢量。
分別為兩齒輪第i對齒面參考點相對于S1、S2坐標(biāo)系的彈性變形速度矢量。




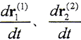 都不為零,因此對嚙入和嚙出齒面,嚙合基本方程為
都不為零,因此對嚙入和嚙出齒面,嚙合基本方程為
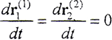 ,(3-4-10)式成為
,(3-4-10)式成為