第2章 滾柱活齒傳動嚙合特性及潤滑性能
2.1 引言
滾柱活齒傳動由于同時具有徑向尺寸小、承載能力高、結(jié)構(gòu)緊湊、傳動效率高等優(yōu)點,因此在石油鉆采及管道工程中具有廣闊的應(yīng)用前景。但目前對它的理論研究還很不完善,使得人們對它的設(shè)計還只能建立在經(jīng)驗和預(yù)估的基礎(chǔ)上,所以對其進行理論研究對于深刻理解和更好地應(yīng)用滾柱活齒傳動具有重要意義。
本章將對滾柱活齒傳動的嚙合特性及潤滑性能進行分析。首先根據(jù)相對運動關(guān)系,推導(dǎo)中心輪齒廓方程,并分析活齒中心運動軌跡曲率的特點,再根據(jù)彈性力學(xué)理論和變形協(xié)調(diào)條件建立其力學(xué)模型,最后分析潤滑狀態(tài)并求解油膜厚度,從而為設(shè)計、分析和加工滾柱活齒傳動減速器奠定理論基礎(chǔ)。
2.2 滾柱活齒傳動原理及特點

滾柱活齒傳動系統(tǒng)(見圖2-la)主要由波發(fā)生器H、活齒G、活齒架S、中心輪R四個部分組成。如圖2-lb所示,滾柱活齒傳動系統(tǒng)在工作時,輸入驅(qū)動力后,輸入軸以等角速度ωH,逆時針旋轉(zhuǎn),從而帶動波發(fā)生器使其幾何中心O′繞旋轉(zhuǎn)中心O以同樣角速度旋轉(zhuǎn),波發(fā)生器半徑變化的輪廓曲線產(chǎn)生徑向推力,迫使與中心輪工作齒廓接觸的諸活齒,在沿活齒架徑向?qū)Р垡苿拥耐瑫r,沿著中心輪工作齒廓滑滾,并通過活齒架的徑向?qū)Р弁苿踊铨X架以勻速ωS逆時針轉(zhuǎn)動,于是滾柱活齒傳動完成了輸入速度ωH、輸出速度ωS的轉(zhuǎn)速變換運動。而與中心輪非工作齒廓接觸的諸滾柱活齒,在活齒架徑向?qū)Р弁苿酉拢樞虻胤祷氐綄?dǎo)槽內(nèi)工作起始位置,從而分別完成了各自的運動循環(huán)。
由滾柱活齒傳動的結(jié)構(gòu)可知,滾柱活齒G是個三副件,它與中心輪R、波發(fā)生器H和活齒架S形成了三個高副,所以研究滾柱活齒傳動嚙合狀態(tài)首先要研究一個嚙合副在一個運動循環(huán)中的嚙合過程。對于常用的波幅ZH=1的波發(fā)生器,其輪廓被經(jīng)過幾何中心O′和旋轉(zhuǎn)中心O的連線分為兩部分:升程曲線和回程曲線,它每轉(zhuǎn)一周推動活齒徑向往復(fù)一次,成為嚙合副的一個運動循環(huán)。與升程曲線接觸的活齒在波發(fā)生器的推動下,由中心輪的齒頂向齒根運動,而與回程曲線接觸的活齒則由中心輪的齒根向齒頂運動。波發(fā)生器每轉(zhuǎn)一周推動活齒徑向往復(fù)一次,稱為嚙合副的一個運動循環(huán)。在一個運動循環(huán)中,活齒與中心輪輪齒接觸點的軌跡形成了中心輪R的一個齒。由嚙合副的嚙合過程可知:與波發(fā)生器H的升程曲線接觸的活齒都處于嚙合狀態(tài),而與波發(fā)生器H的回程曲線及遠(yuǎn)停、近停曲線接觸的活齒都處于非嚙合狀態(tài),所以我們將波發(fā)生器H的升程曲線所對的圓心角稱為工作區(qū)域角,工作區(qū)域角內(nèi)為嚙合區(qū),而把它的回程曲線(包括遠(yuǎn)停、近停曲線)所對的圓心角稱為非工作區(qū)域角,非工作區(qū)域角內(nèi)為非嚙合區(qū)。
2.3 中心輪齒廓方程的建立及齒廓仿真
根據(jù)滾柱活齒傳動原理可知:中心輪齒廓曲線是活齒G在運動過程中齒廓曲線族的包絡(luò)線。當(dāng)活齒傳動不發(fā)生頂切時,該包絡(luò)線就是活齒中心運動軌跡的等距線。所以,欲求中心輪齒廓方程就要先求出活齒中心運動軌跡的方程。
2.3.1 活齒中心運動軌跡方程的建立
滾柱活齒傳動的連續(xù)性是靠彼此間存在相差的并聯(lián)嚙合副交替工作來實現(xiàn)的。因為各個并聯(lián)的嚙合副從嚙合開始到結(jié)束的工作過程完全相同,相鄰兩個嚙合副僅差一個相位,所以研究與相位無關(guān)的齒廓方程,可以任選一個活齒作為研究對象。另外,在工作時,需將中心輪R 或活齒架S 固定一個(常固定中心輪R )。
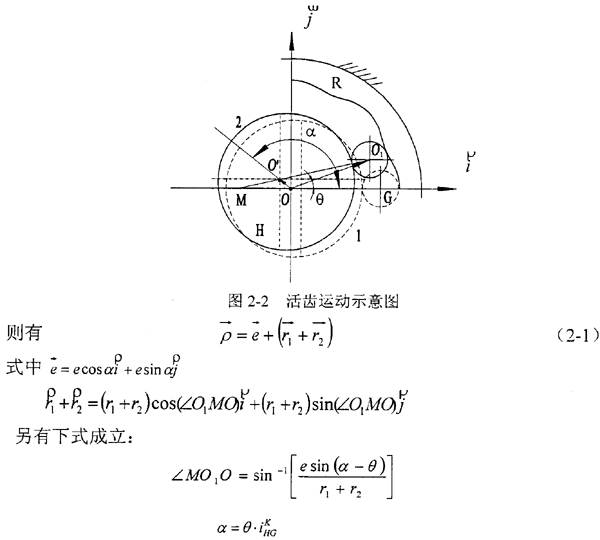
中心輪R 靜止時,與之固連的坐標(biāo)系為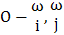 (圖2-2) ,波發(fā)生器H勻速逆時針旋轉(zhuǎn),設(shè)活齒在波發(fā)生器上作純滾動并在中心輪齒廓限制下推動活齒架作勻速逆時針轉(zhuǎn)動。波發(fā)生器H 的幾何中心為O′,活齒G 的幾何中心為O1。在矢量ΔO O′O1中,矢量
(圖2-2) ,波發(fā)生器H勻速逆時針旋轉(zhuǎn),設(shè)活齒在波發(fā)生器上作純滾動并在中心輪齒廓限制下推動活齒架作勻速逆時針轉(zhuǎn)動。波發(fā)生器H 的幾何中心為O′,活齒G 的幾何中心為O1。在矢量ΔO O′O1中,矢量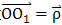 即為所求的活齒中心運動軌跡曲線的徑矢,
即為所求的活齒中心運動軌跡曲線的徑矢, 為波發(fā)生器半徑矢量
為波發(fā)生器半徑矢量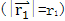 ,r2μ為活齒半徑矢量(|r2μ|=r2),則
,r2μ為活齒半徑矢量(|r2μ|=r2),則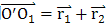 。初始位置1時,
。初始位置1時,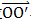 、
、 和iμ軸重合,經(jīng)過一段時間后,波發(fā)生器H 和活齒G 轉(zhuǎn)到位置2時,設(shè)
和iμ軸重合,經(jīng)過一段時間后,波發(fā)生器H 和活齒G 轉(zhuǎn)到位置2時,設(shè)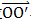 與iμ軸成α角,
與iμ軸成α角, 與iμ軸成θ角。
與iμ軸成θ角。
式中iHGK—中心輪R 固定時,波發(fā)生器輸入、活齒架輸出時的傳動比。
同時為方便計算,令l=e/(r1+r),φ=∠MO1O,則∠O1MO=θ-φ,代入式(2-1)整理得活齒中心軌跡方程為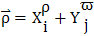 ,即:
,即:
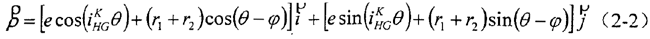
2.3.2 中心輪齒廓方程的建立
在不發(fā)生頂切的情況下,中心輪齒廓曲線就是活齒中心運動軌跡的外等距線,表示為:
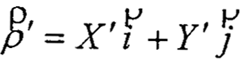
式中ρ'ρ——中心輪齒廓曲線的徑失。
根據(jù)式(2-2),得活齒中心輪齒廓方程為:
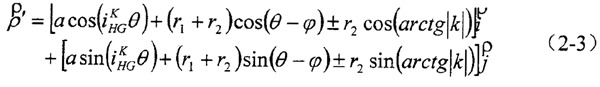
2.3.3 中心輪齒廓仿真
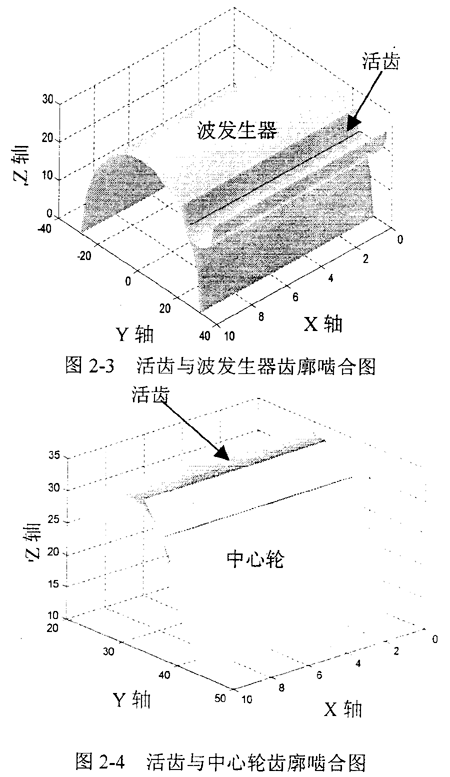
為驗證以上理論推導(dǎo)的正確性并直觀地顯示出活齒傳動中的嚙合情況,擬對其進行仿真研究。為顯示齒廓的三維曲面,將齒廓曲面對應(yīng)的自變量區(qū)域(XOY平面上)劃分為5×34個網(wǎng)格。先由數(shù)學(xué)模型計算出中心輪和活齒齒面上對應(yīng)自變量區(qū)域網(wǎng)格節(jié)點的值,得到齒廓曲面的網(wǎng)格圖,然后采用二維線性插值的方法,得到整個齒廓曲面。同時,比較活齒與中心輪齒廓曲面上對應(yīng)點的坐標(biāo)值,將坐標(biāo)值相同的點(接觸點)在圖象上以另一種顏色顯示,以便觀察接觸的情況。編程采用具有很強矩陣處理功能和繪圖功能的MatLab 語言。
活齒與波發(fā)生器的嚙合情況見圖2-3,可以清楚地看到接觸線為一條直線。從生成的接觸點的坐標(biāo)可以看到,這些點的坐標(biāo)中只有x值變化,而y和z 的坐標(biāo)值相同,也就是這些點在空間上組成了一條平行于x軸的直線,說明活齒與波發(fā)生器之間不但是線接觸,而且這條接觸線也平行于活齒的回轉(zhuǎn)軸。
采用相同算法得到活齒與中心輪嚙合時齒廓曲面的三維圖形(圖2-4 ),同樣可見其接觸線也是一條平行于回轉(zhuǎn)軸的直線。
2.4 活齒中心運動軌跡曲率的確定及其特點
在活齒傳動的嚙合理論分析中,常常要用到中心輪齒廓上任意一點的曲率K,而根據(jù)中心輪齒廓方程直接計算曲率極為復(fù)雜。
另一方面,由于波發(fā)生器的半徑常常遠(yuǎn)大于活齒半徑(通常十幾倍),所以活齒中心運動軌跡曲線上任意一點的曲率僅比它的等距線——中心輪齒廓曲線上對應(yīng)點的曲率略大,在接觸疲勞強度計算中可以近似認(rèn)為相等。這樣不但使活齒的理論分析變得可行,同時也可大大地簡化計算,使之更便于工程應(yīng)用。另外,這樣近似計算的結(jié)果使得到的接觸疲勞強度略偏于安全,設(shè)計更為可靠。
活齒中心運動軌跡的曲率為:
一滾柱活齒傳動減速器,偏心距e =1.5mm,波發(fā)生器半徑r1=30mm,活齒半徑r2=8mm,傳動比iHGK=9。采用MatLab編程,分別得到活齒中心運動軌跡和中心輪齒形(圖2-5)以及活齒中心運動軌跡的曲率K與活齒架旋轉(zhuǎn)過的角度θ之間的關(guān)系曲線(圖2-6)。
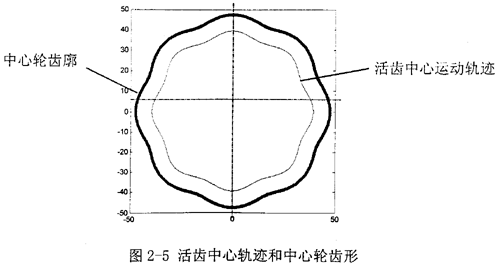

推而廣之,并考慮到中心輪齒廓曲率的變化趨勢與活齒中心運動軌跡相同,可得到中心輪曲率K的特點如下:
(1)由圖2-6中K-θ曲線可以看出,中心輪每一個齒在齒根處曲率最大,曲率半徑最小。沿著齒廓上升的過程中曲率減小到零后,繼續(xù)減小為負(fù)值。到達(dá)齒頂時,曲率最小。
(2)齒頂處曲率的絕對值要小于齒根處的曲率絕對值。也就是說,齒根處的曲率半徑要略小。所以在結(jié)構(gòu)設(shè)計中可用齒根處的曲率半徑來保證不發(fā)生頂切,在強度校核計算中可用齒根處的曲率半徑來計算以使結(jié)果略偏于安全。
2.5 滾柱活齒傳動力學(xué)模型的建立
2.5.1 單個活齒受力分析
波幅ZH=1 的滾柱活齒傳動在理論上每一時刻都有半圈活齒參與嚙合,屬于復(fù)雜的過約束機構(gòu),無法用剛體力學(xué)完全確定,必須根據(jù)彈性力學(xué)理論和變形協(xié)調(diào)條件建立其力學(xué)模型。分析可知,不同活齒在每個運動循環(huán)中受力情況相同,不失一般性,從圖2-la中右側(cè)逆時針任取第j個活齒作研究對象。不計重力和摩擦力,活齒受力如圖2-7 所示。
固定中心輪R,不失一般性,選擇活齒數(shù)ZG與中心輪齒數(shù)ZR之差為1。此時傳動比大小等于活齒個數(shù)。假設(shè)開始時,波發(fā)生器的幾何中心O1在X軸上,該活齒中心在B點,波發(fā)生器以角速度ω逆時針轉(zhuǎn)動。t時刻時,波發(fā)生器轉(zhuǎn)過θ角,該活齒中心運動到Bl點,波發(fā)生器的幾何中心從Ol運動到O2;Fsj、FHj、FKj分別為活齒架、波發(fā)生器、中心輪對該滾柱活齒的法向壓力。
根據(jù)傳動比的定義和波發(fā)生器與活齒間相對運動關(guān)系,得到:
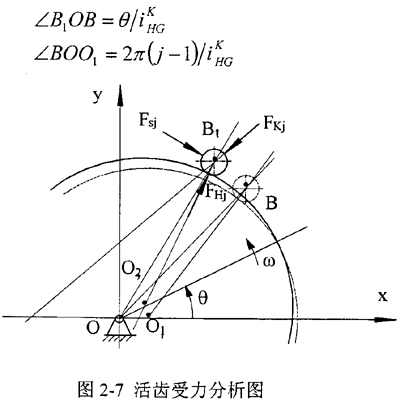
式中iHGK——中心輪固定時,波發(fā)生器輸入、活齒架輸出時的傳動比;
θ——波發(fā)生器逆時針轉(zhuǎn)過的角度。

式中
kn—活齒中心運動軌跡在Bl點處的法線斜率;
ax—活齒中心在X方向的加速度;
ay—活齒中心在Y方向的加速度。
根據(jù)活齒中心運動軌跡方程:

其中dj=(r1+r2)sin∠OO2B1/sin∠B1OO2。每個活齒有3個未知數(shù),共有3ZG個未知數(shù),方程數(shù)為2ZG+l個,需要補充ZG-1個方程,方可求解。
考慮變形協(xié)調(diào)條件,設(shè)第j個活齒的接觸變形量分別為δHj,δKj和δSj,導(dǎo)致活齒中心與旋轉(zhuǎn)中心O的連線OB1轉(zhuǎn)過微小角度θG,反映在坐標(biāo)系中,就是活齒中心B在水平和垂直兩方向微小的位移Bxj和Byj,可列:
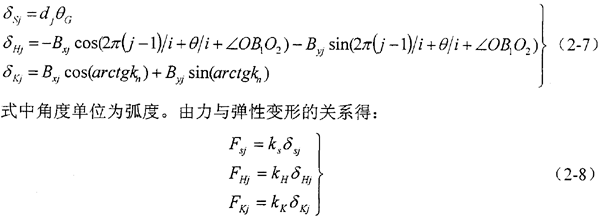
式(2-7)和式(2-8)聯(lián)立,其中未知數(shù)為θG、Bxj和Byj,共有2ZG+l個,而方程共有3ZG個,所以ZG-1為式(2-7)和式(2-8)聯(lián)立后實際補充的方程數(shù),它與式(2-5)和式(2-6)聯(lián)立后需要補充的方程數(shù)相等,所以原方程可解。
2.5.2 雙排結(jié)構(gòu)滾柱活齒受力分析
在實際應(yīng)用中,為平衡掉負(fù)載對支承的徑向作用,一般采用180°對稱布置的雙排結(jié)構(gòu),兩排活齒共用一個活齒架。圖2-8 中O′a′、O″A″分別表示第一排、第二排波發(fā)生器的偏心距。在以下分析中約定:上角標(biāo)“′”表示第一排活齒傳動的參數(shù),上角標(biāo)“″”表示第二排活齒傳動的參數(shù)。T1、T1′和T1″分別表示輸入軸上的總輸入力矩、第一和第二個波發(fā)生器分擔(dān)的輸入力矩。在輸入力矩的作用下,輸入軸和波發(fā)生器發(fā)生扭轉(zhuǎn)變形使兩波發(fā)生器的相位差由理論的180°有了一個相對的變化△φ,從而使兩排活齒的受力情況略有不同,所承擔(dān)的扭矩也不同。為此,引入載荷傳遞不均勻系數(shù)Kp,設(shè)第二排活齒傳遞的扭矩為KpT2,則第一排活齒傳遞扭矩為(l-KP)T2,其中T2為輸出軸上輸出的總扭矩。
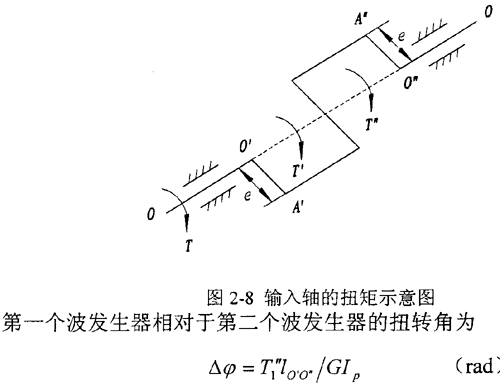
式中l(wèi)O′O″—— 兩波發(fā)生器軸向距離即O′O″距離;
G——材料的剪切彈性模量;
Ip——軸截面極慣性矩,πD4/32(mm4),D為軸直徑;
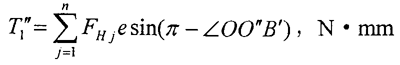
由于輸入軸的扭轉(zhuǎn)變形,使第二個波發(fā)生器相對于第一個波發(fā)生器發(fā)生了△φ的轉(zhuǎn)角,假設(shè)波發(fā)生器固定,由相對運動關(guān)系可知,相當(dāng)于活齒架發(fā)生了△φ/iHGK的偏轉(zhuǎn)角,又因在Tl″的作用下,活齒架發(fā)生了θG″的偏轉(zhuǎn)角,故第二個活齒架的總偏轉(zhuǎn)角為θG″+△φ/iHGK,同時在Tl′作用下活齒架的微轉(zhuǎn)角為θG′,因兩排活齒共用一個活齒架,故得

由公式(2-8),可用Bxj′、Byj′和θG′等2ZG+l個未知量代換式(2-10)中的FHj′、FKj′和FSj′等3ZG個未知量,從而將方程組化為含Bxj′、Byj′、θG′和KP等2ZG+2個未知量的2ZG+1 個方程的方程組。同理可將式(2-11)變換為含Bxj′、Byj′和θG′等2ZG+1個未知量的2ZG+l 個方程的方程組,聯(lián)立式(2-9)、(2-10)、( 2-11) ,可得一個含4ZG+3個方程的方程組,而該方程組的未知量Bxj′、Byj′、θG′、Bxj″、Byj″、θG″及KP共有4ZG+3個,故完全可以求解。
2.5.3 計算實例
一特種用途的滾柱活齒減速器,采用雙排結(jié)構(gòu),中心輪固定,波發(fā)生器輸入,活齒架輸出。輸出扭矩為150Nm,輸入軸轉(zhuǎn)速n1=2980rpm,結(jié)構(gòu)參數(shù)為:波發(fā)生器幾何中心相對旋轉(zhuǎn)中心的偏心距e=1.5,波發(fā)生器半徑r1=30,活齒半徑r2=8,活齒數(shù)ZG=9,中心輪齒數(shù)ZR=8,活齒架內(nèi)徑DS=66,外徑DM=86,兩排活齒軸向距離lO′O″=76,活齒長L=60,(長度單位:mm)。 活齒材料為GCr15,密度7.8×10-6kg/mm3,載荷不均勻系數(shù)kp=0.4953。根據(jù)公式(2-5)~(2-11),采用牛頓法求解聯(lián)立方程組。為方便初值的確定,先用高斯法求解,將所得的解作為初始值,然后再用牛頓法求解方程組。采用MatLab編程計算,當(dāng)OO1逆時針轉(zhuǎn)過4°時,各力情況見表2-1。
表2-1 實例的計算結(jié)果
| 第一排活齒 |
第二排活齒 |
| 活齒 |
FH |
FK |
FS |
kp |
FH |
FK |
FS |
| 2 |
1.064 |
1.362 |
1.142 |
0.4953 |
1.027 |
1.393 |
1.297 |
| 3 |
1.002 |
1.176 |
1.120 |
0.993 |
1.133 |
1.099 |
| 4 |
0.883 |
0.971 |
0.983 |
0.871 |
0.983 |
0.896 |
| 5 |
0.781 |
0.826 |
0.651 |
0.779 |
1.120 |
0.912 |
注:因第一個活齒開始進入非工作齒廓,故不考慮它的受力情況。
2.6 滾柱活齒傳動的潤滑性能分析
減速器的潤滑狀態(tài)直接影響其摩擦和磨損的程度,進而對其壽命產(chǎn)生影響。為了準(zhǔn)確把握和評價滾柱活齒減速器的潤滑特性,本節(jié)擬對其進行分析,判斷其潤滑狀態(tài),求解油膜厚度。
2.6.1 潤滑狀態(tài)的判斷及油膜厚度的計算
滾柱活齒減速器在工作時,活齒與活齒架、活齒與波發(fā)生器、活齒與中心輪之間皆為線接觸高副,且減速器內(nèi)充滿潤滑油,這時的各運動副之間的潤滑屬于既要考慮潤滑油的粘壓效應(yīng),又要考慮高副構(gòu)件表面彈性變形的彈性流體動力潤滑(EHL)。同時,由于高副間的相對運動要產(chǎn)生溫升以及工作在采油井下,在分析時,必須要考慮潤滑油及高副運動件之間的熱平衡,也就是屬于熱彈流問題。所以,本潤滑屬于線接觸穩(wěn)態(tài)全膜熱彈流潤滑,潤滑油按牛頓流體處理。先分析波發(fā)生器與活齒之間的潤滑情況,活齒與中心輪、活齒與活齒架之間的情況完全類似,只是計算時幾何參數(shù)略有不同。
根據(jù)計算流體動力潤滑膜厚的張鵬順統(tǒng)一公式,最小膜厚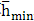 和中心膜厚
和中心膜厚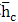 為:
為:

u——接觸體表面的平均速度(卷吸速度)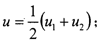 ;
;
w——單位接觸線長度上的載荷。
山于活齒與中心輪、活齒架和波發(fā)生器之間存在高速滾動,而且在滾動的同時又伴有相當(dāng)?shù)幕瑒樱詿嵝?yīng)不能忽略。
引入熱承載參數(shù)L,它反映潤滑劑熱特性和滾動速度的大小。

式中
δ——粘溫系數(shù);
K——潤滑油導(dǎo)熱率。
考慮熱效應(yīng)時的最小膜厚為Hin,對應(yīng)的等溫的膜厚為Hmin,ISO,則有:
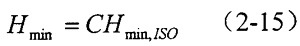
式中
C——考慮入口剪切熱的修正因子,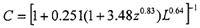 ;
;
z——滑滾比,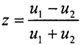 。
。
以上是針對波發(fā)生器和活齒之間的潤滑情況分析,對于活齒和中心輪之間以及活齒和活齒架之間的情況完全相同,不同的是當(dāng)量半徑和卷吸速度的計算。
2.6.2計算實例
一滾柱活齒減速器,波發(fā)生器半徑rl=30mm,偏心距e=1.5mm,活齒半徑r2=8mm,傳動i=9,波發(fā)生器轉(zhuǎn)速n=2850rpm,材料的彈性模量E1=E1=2.1×1011N/m2,泊松比v1=v2=0.3,粘壓系數(shù)α=2.2×10-8Pa-1,常壓下潤滑油的粘度粉η=35.8×10-3N·S/m,粘溫系數(shù)δ=0.017。
由公式(2-12)~(2-15),編程計算得t=0.6316,根據(jù)潤滑狀態(tài)的判斷條件,當(dāng)5/9<t<1時,是彈性流體動力潤滑狀態(tài),且常溫時最小油膜厚度為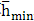 =0.8920μm,中心膜厚為
=0.8920μm,中心膜厚為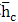 =1.0989μm。考慮熱效應(yīng)時的修正因子為C= 0.7148 ,最小油膜厚度為
=1.0989μm。考慮熱效應(yīng)時的修正因子為C= 0.7148 ,最小油膜厚度為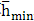 =0.6376μm。
=0.6376μm。
2.7 本章小結(jié)
1.根據(jù)滾柱活齒傳動的相對運動關(guān)系,建立了活齒中心運動軌跡方程和中心輪齒廓方程,并仿真出齒廓曲面;給出了活齒中心運動軌跡曲線上任意一點曲率K 的計算方法,分析了中心輪在齒根和齒頂處曲率半徑的特點。
2.在單個活齒受力分析的基礎(chǔ)上,根據(jù)變形協(xié)調(diào)條件,給出了滾柱活齒的受力計算公式,為滾柱活齒傳動的強度設(shè)計奠定了基礎(chǔ)。
3.深入分析了滾柱活齒傳動的潤滑性能,給出了活齒與波發(fā)生器之間的油膜厚度的計算方法,確定了潤滑狀態(tài)是屬于線接觸穩(wěn)態(tài)全膜熱彈流潤滑。
4.以一具體滾柱活齒減速器為例,得到了活齒中心運動軌跡上任意一點曲率K與活齒架旋轉(zhuǎn)過的角度θ之間的關(guān)系曲線,求出了兩排活齒的受力情況,計算出活齒與波發(fā)生器之間的油膜厚度。
上一頁
下一頁


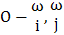 (圖2-2) ,波發(fā)生器H勻速逆時針旋轉(zhuǎn),設(shè)活齒在波發(fā)生器上作純滾動并在中心輪齒廓限制下推動活齒架作勻速逆時針轉(zhuǎn)動。波發(fā)生器H 的幾何中心為O′,活齒G 的幾何中心為O1。在矢量ΔO O′O1中,矢量
(圖2-2) ,波發(fā)生器H勻速逆時針旋轉(zhuǎn),設(shè)活齒在波發(fā)生器上作純滾動并在中心輪齒廓限制下推動活齒架作勻速逆時針轉(zhuǎn)動。波發(fā)生器H 的幾何中心為O′,活齒G 的幾何中心為O1。在矢量ΔO O′O1中,矢量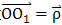 即為所求的活齒中心運動軌跡曲線的徑矢,
即為所求的活齒中心運動軌跡曲線的徑矢, 為波發(fā)生器半徑矢量
為波發(fā)生器半徑矢量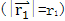 ,r2μ為活齒半徑矢量(|r2μ|=r2),則
,r2μ為活齒半徑矢量(|r2μ|=r2),則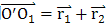 。初始位置1時,
。初始位置1時,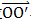 、
、 和iμ軸重合,經(jīng)過一段時間后,波發(fā)生器H 和活齒G 轉(zhuǎn)到位置2時,設(shè)
和iμ軸重合,經(jīng)過一段時間后,波發(fā)生器H 和活齒G 轉(zhuǎn)到位置2時,設(shè)
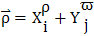 ,即:
,即: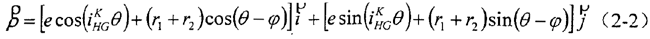
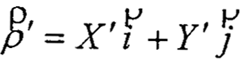
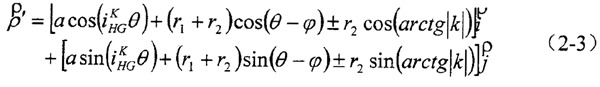

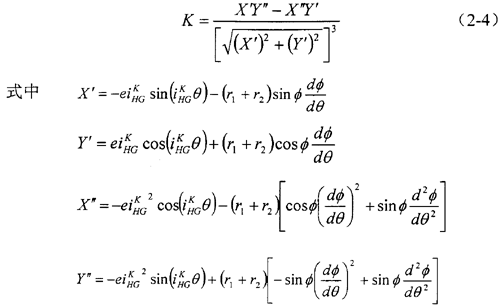





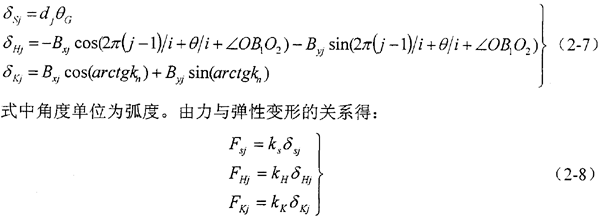

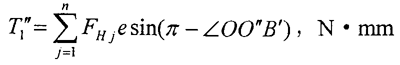

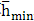 和中心膜厚
和中心膜厚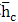 為:
為:
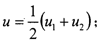 ;
;
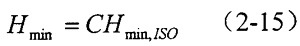
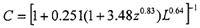 ;
;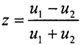 。
。