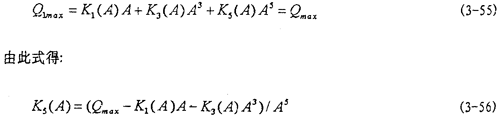然后用線性參數辨識法和非線性參數辨識法，根據上面已經得到的各個工況下K1（A)，K3（A），K5（A),C(A,f)和n（A,f）的數值對（3-48）、（3-49）、（3-50）式中各參數進行辨識，將辨識得到各參數代入（3-48）、（3-49）和（3-50）式得：
關于K5（A)的辨識采用以下方法：
當位移x達到最大值A時，聯軸器恢復力Q達到最大值，彈性恢復力也達最大值，此時有：
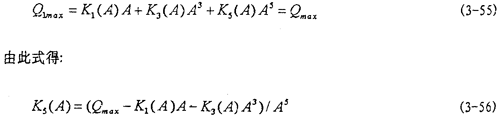
式中K1（A)，K3（A）已求得。由試驗遲滯回線恢復力最大值與振幅的數據，可辨識出（3-56）式的
為：
（A）=-5.16965×10-5A7+2.21538×10-5A6+0.0241174A5-0.375207A4+2.55596A3-8.88624A2+16.8085A-
8.37136 （3-57）
將（3-51)、(3-52）和（3-57）式代人（3-56）即求得K5（A)。至此，(3-47）式中的各參數函數已全部辨識出。將這些參數代入(3-47）式就得到聯軸器恢復力數學模型。
二、結果分析與比較
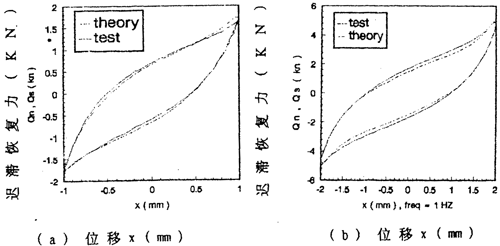
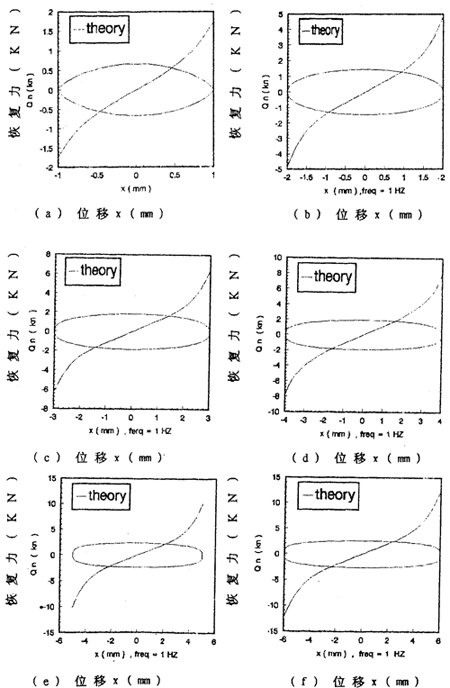
由數學模型（3-47) 計算可以得到不同激勵頻率和振幅下聯軸器恢復力遲滯回線數據，為了證實（3-47）的正確性，下面畫出頻率為1赫茲、振幅為1～8毫米各工況下數學模型計算的理論數據和試驗數據表示的遲滯回線圖，如圖(3-8)(a）～（h)（見51～52頁）所示，圖中虛線為理論回線，實線為試驗遲滯回線。從圖中可知，理論遲滯回線十分接近試驗遲滯回線，由此可以說明建立的聯軸器數學模型（3-47）式可較好地描述恢復力隨振幅A頻率f、瞬時位移x和速度
變化的規律，較圓滿地解決了聯軸器恢復力建模與參數函數辨識的難題。
為了進一步分析聯軸器的阻尼特性并與用擬合分析解法和阻尼等效原理建立的數學模型（3-12）、（3-13）、（3-14）作比較，畫出由數學模型（3-47）式分別描述的彈生恢復力
1和阻尼力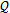>2的曲線圖，如圖（3-9）a）～（h）所示，圖中單值曲線為彈性恢復力1。雙值閉合曲線為阻尼力2。
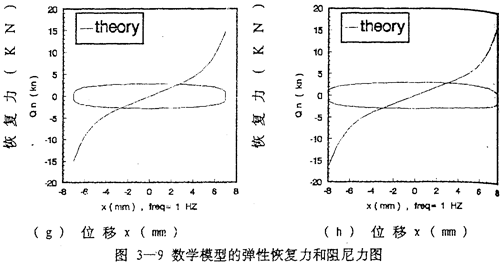
(1).從圖3-9(a）-（h）中可以看到：雙值閉合曲線的形狀隨振幅的增大，從橄欖形變成橢圓形，再變成棒槌形。說明聯軸器的阻尼成分不是單一的，而是多種阻尼的組合，這些阻尼在不同的振幅下出現的大小比例不同，振幅為1毫米時，見圖3-9(a）圖，“高次”阻尼成分較多，而干摩擦阻尼和粘性阻尼成分較少，這時阻尼力閉合曲線的形狀呈橄欖形，這是因為振幅較小時，聯軸器彈性元件中的鋼絲繩股與股之間所受的力和位移都較小，還沒有產生相對滑移。隨著彈性元件受力增加、位移增加，鋼絲繩股與股之間的摩擦力增大，局部出現滑移，這種狀態下，聯軸器的阻尼成分以粘性阻尼為主，摩擦阻尼次之，閉合曲線，即阻尼力曲線的形狀呈橢圓形，振幅為2-4毫米。見圖（3-9)(b）～（d)，隨著聯軸器受力的進一步增大，位移隨之增加，鋼絲繩股與股之間出現大的相對滑移，阻尼力曲線的形狀呈棒縋形，介于橢圓與矩形之間，但更加接近矩形，這說明此種情況下，聯軸器的阻尼成分以干摩擦阻尼為主，粘性阻尼為次，振幅介于5-8毫米之間，見圖（3-9)(e）～（h)。
(2).表3-1列出阻尼成分函數n（A,f）在1赫茲時，隨振幅變化的數值，對應于圖3-9中各閉合曲線。
從表中可以看出，當n（A,f)>1時，阻尼成分以“高次”阻尼為主，阻尼力曲線呈橄攬形；當0.6<n(A,f)<l時，阻尼成分以粘性阻尼為主，阻尼力曲線呈橢圓形；當0＜n（A,f)＜0.6時，阻尼成分以干摩擦為主，粘性阻尼次之，阻尼力呈棒縋形；當n(A,f)=0時，阻尼成分將變成純粹的干摩擦，由n（A,f）的值變化可知，產生這種情況的可能性很小。由此可以知道，阻尼成分函數n(A,f)控制阻尼力曲線的形狀。
（3）.從圖3～9中各圖可知：阻尼力的大小隨振動位移x變化而變化，實質上阻尼力的大小隨振動速度
的大小變化。在x等于零時，速度最大，所以，阻尼力的絕對值達到最大，在位移x為振幅值A時，速度為零，阻尼力零。
（4）.表3-2列出阻尼函數C（A,f）在1赫茲時，隨振幅變化的數值，對應于圖3-9中各閉合曲線。從表中可知：隨著振幅A的增大，阻尼函數隨之增大，這說明了聯軸器的阻尼耗能隨振幅增大而增大的原因。
表3-1 阻尼成分函數n(A,f)控制阻尼力曲線的形狀。
| A（mm） |
1 |
2 |
3 |
4 |
| n(A,f) |
1.376734 |
0.9397465 |
0.7516245 |
0.6414627 |
| A（mm） |
5 |
6 |
7 |
8 |
| n(A,f) |
0.5672612 |
0.5130523 |
0.4712813 |
0.4378568 |
表3-2 阻尼函數C（A,f）隨振幅A變化表
| A（mm） |
1 |
2 |
3 |
4 |
| C（A,f） |
6.814558×10-2 |
1.351919×10-1 |
2.018296×10-1 |
2.682031×10-1 |
| A（mm） |
5 |
6 |
7 |
8 |
| C（A,f） |
3.343811×10-1 |
4.004035×10-1 |
4.662969×10-1 |
5.3208×10-1 |
將數學模型（3-57）與數學模型（3-12）、（3-13）、（3-41）進行比較，可知
（1）.數學模型（3-57）中的彈性恢復力模型中有三個剛度函數，而數學模型（3-12）中的彈性恢復力模型中有五個剛度函數，因此前者較后者簡單，但精度不如后者。
（2）.數學模型（3-57）中的阻尼力中由于引入了阻尼成分函數n（A,f），因而該阻尼力模型能揭示聯軸器阻尼成分的組成和變化規律；而數學模型（3-41）中的阻力模型是在阻尼等效原理的基礎上建立起來的，因而不能描述聯軸器中復雜的阻尼成分。由此可見數學模型（3-57）和數學模型（3-12）（3-13）（3-41）各自有自己的優點和不足，后者能較好地描述動剛度，前者能較好地描述阻尼。
（3）.數學模型（3-57）在參數辨識時，采用的方法是整體辨識法，即將聯軸器的彈性恢復力和阻尼力中的各未知參數放在一起進行辨識，由于一次需辨識的參數較多。若再考慮K7（A)，K9（A），將使辨識難度大大增加，故在（3-57)模型中只考慮了K1（A)，K3（A)，K5（A）。而數學模型（3-12）（3-13）(3一41）的參數辨識，采取的方法是擬合分解法，即將聯軸器的恢復力分解成彈性恢復力和阻尼力兩個式子，分別對其未知參數進行辨識。
在后面的幾章中，為了計算簡便些，將采用數學模型（3-12)(3-41)。
3-6 小結
本章在鋼絲繩彈性聯軸器振動試驗數據進行分析和處理的基礎上，圍繞聯軸器的建模和參數辨識作了以下工作：
(1）在Ko等人工作的基礎上，發展了一種用于非線性遲滯特性系統研究的擬合分解法。用此法將聯軸器非線性恢復力遲滯回線擬合分解成兩部分：非遲滯非線性彈性恢復力和純遲滯非線性阻尼力，為分別研究非線性彈性恢復力和非線性阻尼力的特性創造條件，并將Ko法只能辨識三個階次動剛度的方法發展為能辨識五個或更多個階次動剛度，為描述大位移強非線性的遲滯特性提供了可行的方法。
(2）針對聯軸器動剛度和阻尼是振幅和頻率的非線性函數，但當頻率增大到一定值后，動剛度和阻尼僅為振幅的非線性函數的特點，分別提出了不受頻率影響和受頻率影響的非線性彈性恢復力數學模型和非線性阻尼力模型（3-11）、(3-14）式和（3-18）、(3-21）式。根據對聯軸器非線性遲滯回線隨振幅和頻率變化規律的分析，認為提出的數學模型能較合理和客觀地描述非線性彈性恢復力和阻尼力的變化規律。
(3）研究了聯軸器阻尼耗能特性，提出了阻尼耗能僅受振幅影響和同時受振幅與頻率影響的數學模型（3-38）和（3-43）式。在對聯軸器非線性遲滯回線面積（即阻尼耗能）進行數值積分的基礎上，經過非線性參數辨識，得出了(3-38）和（3-43）模型中的各參數。從而得到了聯軸器阻尼耗能隨振幅的增大而增大，隨頻率的增大而減小的函數關系式。
(4）以聯軸器非線性阻尼耗能研究為基礎，根據阻尼等效原理，研究并建立了聯軸器阻尼僅受振幅影響和同時受振幅和頻率影響的數學模型（3-40）和(3-45)，經過參數辨識得出了模型中的各參數，由此弄清楚了聯軸器阻尼隨頻率和振幅變化的規律，在此基礎上，建立了聯軸器非線性阻尼力的數學模型（3-41）和（3-46）式。
(5）對不受頻率影響的非線性彈性恢復力數學模型（3-11）式中的參數進行辨識，得出了五個動剛度函數的表達式（3-27)，分析表明，聯軸器的動剛度具有剛度軟化的特性，這一特性對防沖減振降噪有利。
(6）對不受頻率影響的非線性阻尼力數學模型（3-14）式和受頻率影響的非線性彈性恢復力數學模型（3-18）及（3-21）式進行了辨識，由于辨識算法的不合適，未能辨識出各參數，為了解決此辨識問題，有待于尋找新的和有效的辨識算法。對聯軸器非線性遲滯特性的分析后，仍認為（3-14）、（3-18）和（3-21）式能合理地描述聯軸器非線性彈性恢復力和阻尼力。由于頻率影響范圍很小，在實際計算中，用非線性彈性恢復力數學模型（3-11）、(3-27）式和非線性阻尼力數學模型（3-41）是完全可行的。
(7）對聯軸器試驗結果和前面關于聯軸器建模與參數辨識工作進行進一步深人分析后，提出了聯軸器恢復力新數學模型（3-47)，采取未知參數整體辨識法，用Marquardt非線性參數辨識方法，成功地辨識出了式（3一47）中各參數。模型（3-47）的優點是阻尼成分函數n(A,f）的引人使得它能全面地揭示聯軸器中的阻尼情況。
上一頁
下一頁
