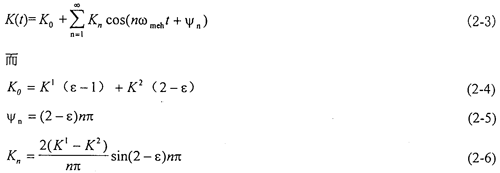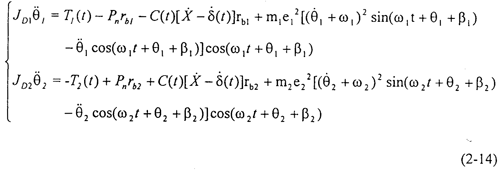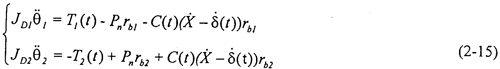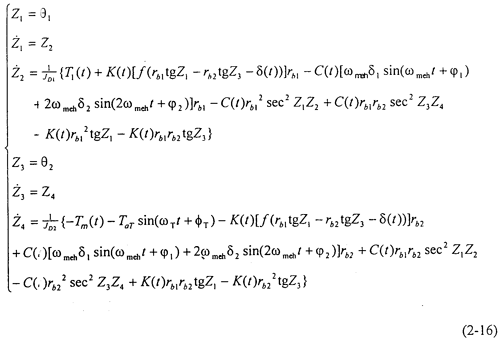第2章 齒輪故障振動的研究
齒輪是機械傳動系統的主要部件，它已被廣泛地應用在旋轉機械及動力傳輸裝置中。齒輪在進行嚙合傳動時，由于外載荷變化、齒輪加工誤差、齒輪嚙合剛度的時變性及嚙合沖擊等因素的影響，齒輪將產生振動。齒輪在振動時構成一個線性時變或非線性時變系統。齒輪在傳動過程中，隨著齒面磨損的擴展，齒輪的齒形誤差、基節誤差和齒側間隙也將增加。齒輪齒側間隙對齒輪振動特性影響的研究，國外起始于1967年K Nakamura的研究，主要利用數值仿真從時域分析研究了齒輪系統的振動特性。近年來國外A Kahlarman等學者從頻域上研究了一定齒側間隙對齒輪幅頻特性的影響，并從實驗上驗證了當存在齒輪側隙時，一個齒輪-傳動軸-支撐軸承系統會產生亞諧和超諧共振。本章在建立齒輪振動微分方程的基礎上，用變步長Runge-Kutta法求出了存在間隙時齒輪振動的時程響應的數值解，并用FFT方法求出時程響應的幅值譜，對在非共振情況下齒輪側隙和載荷的變化對齒輪振動頻率的影響進行了研究。研究結果表明，齒側間隙的變化對齒輪的振動故障頻率成份有很大的影響；齒側間隙的值一定時，如果齒輪的工作轉速和工作載荷發生改變時，齒輪的振動故障頻率成份也有改變。該結果對齒輪的故障診斷和齒輪傳動系統動態設計有重要的意義。
此外，本章還對齒輪偏心質量對齒輪扭轉振動的影響進行了分析研究，并分析了頻譜特征。
2.1 齒輪振動力學模型及嚙合力分析
設有一對齒輪傳動，齒輪1為主動齒輪，齒輪2為從動齒輪，它們分別有一偏心質量ml和m2，振動力學模型見圖2-l。設主動齒輪的扭轉振動角位移、角速度、角加速度和旋轉角速度分別為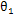
、
、
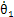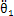和ω1，從動齒輪的扭轉振動角位移、角速度、角加速度和旋轉角速度分別為
、
、
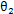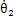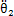和ω2，則有ω1=iω2(i為齒輪傳動比）。
為了研究問題的方便，特作如下假設：
(l）齒輪的支撐軸又短又粗，近似為剛性軸，故不考慮其橫向振動及扭轉振動；
(2）滾動軸承剛度較大，作為剛性支撐處理并忽略軸及軸承的阻尼。
作用在主、從動齒輪的力矩分析如下：
（1）作用在主動齒輪上的驅動力矩T1（t）是常數，即T1（t）=C；而作用在從動齒輪上的工作阻力矩T2（t）可看作一個恒量Tm與幅值為TaT簡弦變量之和：
T2（t）=Tm+TaTsin（ωTt+фT） （2-1）
式中ωT、фT-分別為從動齒輪上的工作阻力矩T2（t）變化圓頻率和初始相位角。
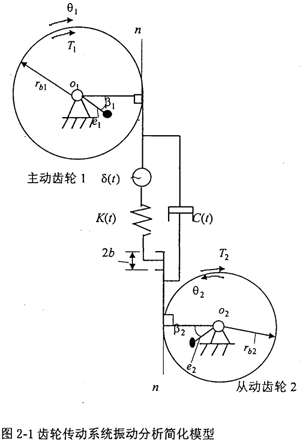
圖2-1中，rb1——主動齒輪基圓半徑；rb2——從動齒輪基圓半徑；K（t）——齒輪嚙合剛度；e1——主動齒輪偏心距；e2——從動齒輪偏心距；β1——主動齒輪不平衡質量的初始角度；β2——從動齒輪不平衡質量的初始角度；δ（t）——齒輪的綜合誤差；JD1——主動齒輪轉動慣量；JD2——從動齒輪轉動慣量；C（t）——齒輪阻尼系數；b——齒側間隙；n-n——齒輪嚙合線方向。
（2）作用在主、從動齒輪間的動態嚙合力及嚙合力矩
i）當不考慮齒側間隙時，動態嚙合力：
Pn=K（t）[X-δ（t）] （2-2）
式中X=rb1tgθ1-rb2tgθ2為主、從動齒輪間的相對振動位移；K（t）為齒輪嚙合剛度，近似視為矩形波，可展為富氏級數：
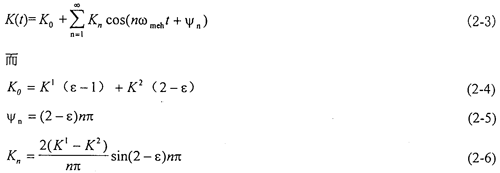
式中：ε——重合度；ωmeh——齒輪嚙合頻率；Kn——齒輪剛度諧波項；K1——單對齒嚙合剛度；K2——兩對齒嚙合剛度；Ψn——齒輪剛度諧波項相位。
一對齒輪的綜合誤差δ（t）也可展為富氏級數：
式中：δn——齒輪誤差諧波系數；
——齒輪誤差諧波項相比；
嚙合力矩Pnrbi （i=1，2）
ii）當考慮齒側間隙時，動態嚙合力：
Pn= K（t）f（rb1tgθ1- rb2tgθ2-δ（t））= K（t）f（t） （2-8）
其中f（t）為分段非線性函數，可表示為如下形式：
（3）阻尼力矩：
C（t）（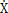
-
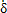（t））rb1 （i=1，2）（不考慮齒側間隙） （2-10）
或C（t）f′（t）rb1 （i=1，2）（考慮齒側間隙） （2-11）
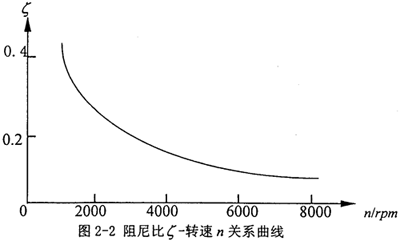
其中：齒輪阻尼系數C（t）=2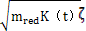
，mred——嚙合齒輪當量質量。阻尼比
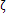根據圖2-2取值。阻尼系數C（t）也可根據下列公式取值：
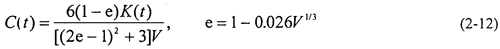
式中：e——中間變量：V為齒面間相對滑動速度。
（4）由不平衡質量即偏心質量造成的附加力（嚙合力方向）：
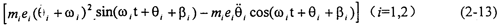
2.2 齒輪振動動力學方程
根據上節單級齒輪系統的受力分析，可得θ1、θ2兩自由度主從動齒輪振動微分方程：
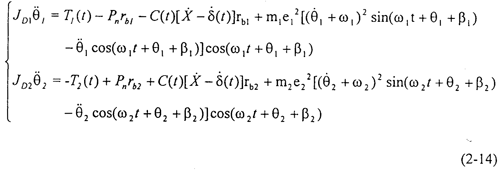
式中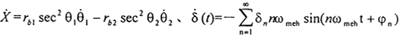
。很明顯，由于θ，
，
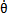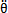前面的系數和時變剛度K（t）、非線性函數f（t）及θ，
有關，不是常數，故方程組（2-14）是一個非線性時方程組。
2.3 方程數值解法及齒輪齒側間隙的振動頻譜特征
當不考慮偏心質量，而只考慮存在齒輪齒側間隙時，方程組（2-14）可化為：
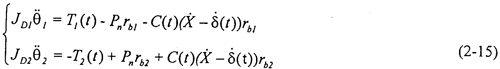
由于上式是一個非線性時變方程組，它的理論解無法得出，故采用數值解法求解。為了便于計算，將方程組（2-15）轉化到狀態空間中，將方程組表達成：
=fi（Z1，Z2，Z3，Z4），i=1，2，3，4，則原方程組可表達成：
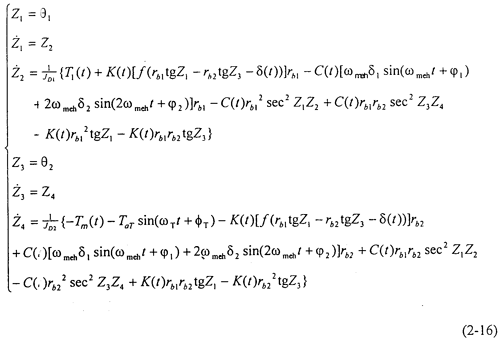
上一頁
下一頁
